Classification

The taxonomies used by TROEPS can be manipulated in order to find adequate places for objects and classes in a given category or for building (upon particular criteria) a taxonomy from the instances of the concept. Each functionality is presented in detail before giving a complete example.

Instance classification

Classification is a suggestion mechanism, but instead of guessing the value of an object field, it tries to find the possible classes for an object to migrate from its current class to a lower (i.e. more specific) class. It is based on matching the field values of the instance to be classified with the current candidate class description. The classification takes place in each viewpoint along the suitable hierarchy and uses bridges to jump from one class in a viewpoint to another one in another viewpoint.
Starting from the current belonging class of the instance in a given viewpoint, the classification mechanism scans all of its subclasses and determines, for each of them, if it is possible, unknown or impossible. A class is:
When a class reveals itself impossible, all its sub-classes are labelled impossible too. Thus, the algorithm iterates on every possible or unknown sub-classes, and ends after it has reached the leaves of the hierarchy. When the classification labels a class which is also the only source of a bridge, as possible or unknown, it deduces that the destination class of the bridge (in another viewpoint) is possible or unknown too. If this is not possible (because the object does not satisfy the constraints of the destination), the initial object is finally labelled as impossible .
The function provided below constitutes the minimal classification service in TROEPS. Improvements are planned including:

Interface

Screendump 46: Classification initialisation.

Screendump 47: Classification result. Classes are displayed in either red (impossible), yellow (unknown) or green (possible). As a result of classification, clicking on a class will access to that class while when used in attach query (see Screendump 32 ), it will attach the object to the selected class.

API

(tr-classify object rest: views ) function in [libtrp]

-> ( ( ( class* ) ( class* ) . ( class* ) )* ), object object nao,views { conceptview nakv* } ivsp
Returns, for each of the provided concept viewpoints views -- and if none is provided, for each of the views of the concept --, the sets of possible, unknown and impossible classes for the object object.
(tr-attachable object class) function in [libtrp]

-> symbol: {imp, unk, pos}, object object nao,class class nac,ivc
Returns a value among pos, unk and imp indicating if the object object is attachable to the class class. Note that if the class class is not a subclass of the current object class under the concept, the returned value is imp.

Examples

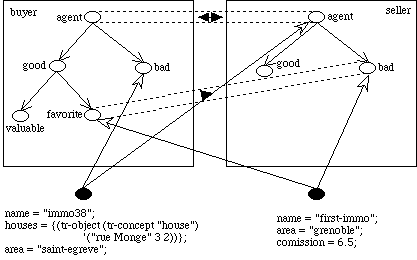
Figure 11: At the end of the complete example session, the resulting situation is presented here. 
? (tr-classify (tr-object (tr-concept "agent") '("first-immo")))
= ((((tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
    ())
   (((tr-class (tr-conceptview (tr-concept "agent") "seller") "bad"))
    ()))
? (tr-classify (tr-object (tr-concept "agent") '("immo38")))
= ((((tr-class (tr-conceptview (tr-concept "agent") "buyer") "bad"))
    ())
   (((tr-class (tr-conceptview (tr-concept "agent") "seller") "agent")
     (tr-class (tr-conceptview (tr-concept "agent") "seller") "bad")
     (tr-class (tr-conceptview (tr-concept "agent") "seller") "good"))
    ()))
? (tr-attachable
    (tr-object (tr-concept "agent") '("immo38"))
	 (tr-class (tr-conceptview (tr-concept "agent") "buyer") "good"))
= imp
? (tr-attachable
    (tr-object (tr-concept "agent") '("immo38"))
	 (tr-class (tr-conceptview (tr-concept "agent") "buyer") "bad"))
= pos
? (tr-attachable
    (tr-object (tr-concept "agent") '("immo38"))
	 (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent"))
= pos
? (tr-attachable
    (tr-object (tr-concept "agent") '("immo38"))
	 (tr-class (tr-conceptview (tr-concept "agent") "seller") "good"))
= pos
? (tr-attachable
    (tr-object (tr-concept "agent") '("first-immo"))
	 (tr-class (tr-conceptview (tr-concept "agent") "buyer") "good"))
= pos

Categorisation

Categorisation consists in inferring the possible positions, in a taxonomy, for a particular class definition. This capability is not provided yet.

Clustering

Clustering consists in organising a set of objects into one or several taxonomies. Clustering methods divide the set of objects into previously unknown classes whereby the main principle may be summarized as follows : the most similar objects are put in the same class and the less similar ones in distinct classes. A function of proximity is used to evaluate the likeness degree of pair of objects. In TROEPS, the clustering facility is based on a universal dissimilarity among the objects manipulated by the system, it can therefore cluster the objects of any concept and return the result as a taxonomy of intensionnally described classes. An environment to host various methods for automatic taxonomy construction, T-TREE, is included in TROEPS.
A detailled account of clustering is given here. However, it can be summarised as follows:
For performing this, the system will, for each viewpoint, in a relevant order, compute the dissimilarity between each pair of objects of the concept. This will depend on the dissimilarity between their field values and the weights applied to field by the dissimilarity measure. Then, the system will aggregate objects into sets (the most similar objects first) and the sets will be aggregated into supersets (forming a taxonomy). Last, all these sets will be provided by class descriptions. This is the resulting taxonomy.

Dissimilarity

The aim of a proximity measure is to evaluate to what extent a pair of objects are alike (or unlike) with respect to the available information about them. Within an object model this information may be extracted either from object fields values or from the class taxonomy of the underlying concept (the mutual position of objects within the taxonomy).
In both cases the comparison of a pair of objects takes advantage of the fundamental principle of the object paradigm, which is the hierarchical organisation of the manipulated entities. Thus, the T-TREE built-in dissimilarity measure, called topological, is based on the fundamental principle of the object paradigm: organising the manipulated entities in a hierarchical manner. It relies on universally available relationships: sub-typing and class specialisation.
For a given pair of objects, the topological dissimilarity is computed with respect to their field values. First, a field-level function computes the differences between the respective pairs of field values. Then, an object-level function combines the values computed in this way into a single global result that caracterizes the compared objects.
The contribution of a field to the global dissimilarity value depends on the nature of the field domain. For abstract data types, i.e. primitive value domains, this contribution is computed on the hierarchical structure of meaningful sub-domains. In fact, given a pair of values, their dissimilarity is based on the relative size of their smallest common sub-domain. The size of a (sub-)domain is the number of domain values it includes. Thus the size of an integer interval [0 2] is 3 as there are three values, 0, 1, and 2. Surprisingly, when taken over an integer domain, the interval [1 1] is of size 1, whereas on a real one its size is 0. This rather complex way of computing the value dissimilarity has the advantage of being universally applicable on simple data types.
In fact, each basic data type connected to TROEPS (see Appendix 5) is provided with a function computing this value. Furthermore, the generic function, when applied on some standard types like integers, reals, etc. matches the well-known and mostly used distance functions like the arithmetic difference on integers.

For instance, given the three objects of the house concept presented in the following table:
objects \ fields
address
number
floor
house-1
"grenoble"
113
0
house-2
"grenoble"
21
2
house-3
"eybens"
13
4

The topological dissimilarity will compare them with respect to the values of a previously selected sub-set of fields. For instance, if one chooses to use the address, the floor and the number fields, whereby their relative importance (or weights) are 0.5, 0.2 and 0.3 respectively, the following computation can be done.
First, the elementary distance between house-1 and house-2 with respect to the address field is 0, since the field type, string, is of unordered (nominal) type family. Thus, only identical items lead to a 0 value for the difference whereas in other cases that value is 1. Furthermore, the address field differences score to a 1 for both the pairs ( house-1, house-3) and ( house-2, house-3). The remaining two fields are processed, in a similar way. The specific point with floor and number is that their types are numeric (quantitative) and discrete. so the arithmetic difference is taken and a normalisation is performed on it. Starting with the difference on floor for ( house-1, house-2), one first computes their most specific common interval which is [0 2] and corrects it by 1 (the mean of the sizes of [0 0] and [2 2], both scoring to 1). The remaining value is divided by 4, the size of the whole domain which yields 0.5. This exactly corresponds to the normalized arithmetic difference on [0 4].
Thus, during clustering, the dissimilarity between two objects can be computed by aggregating the dissimilarities with regard to each field. Precisely, the dissimilarity between each field value is computed (by the previous method) and a weighted combination of each measure is computed (weights are provided through Screendump 48 ).
For instance, the weighted sum (weighted City block function) of the example above will compute the following values:
d(house-1, house-2) = 0.5 * 0 + 0.2 * 0.5 + 0.3 * 0.92 = 0.1 + 0.276 = 0.376,
d(house-1, house-3) = 0.5 * 1 + 0.2 * 1 + 0.3 * 1 = 0.5 + 0.2 + 0.3 = 1,
d(house-2, house-3) = 0.5 * 1 + 0.2 * 0,5 + 0.3 * 0.08 = 0.5 + 0.1 + 0.024 = 0.624.

The same principle is applied on object-valued fields: the likeness between objects taken as field values depends on their respective positions within the underlying taxonomy. Actualy, a taxonomy provides a set of classes which represent the admissible sub-domains of the whole object domain which is itself defined by the underlying concept. The dissimilarity is measured on the most specific common super-class of both objects. The number of the member objects is taken as class size. Thus, the most specific the common class, the most similar the member objects. Besides, the same computation procedure, i.e. corrections and normalization, applies on both objects and simple values.
For instance, on Figure 13 , the following inter-object dissimilarities may be computed :
d(house-1, house-2) = 0.4,
d(house-1, house-3) = 1,
d(house-2, house-3) = 0.6.

The topological measure allows the various aspects of the concerned objects to be taken into account: the resemblance of objects under different viewpoints are evaluated separately (in function of the length of the shortest path between them in the taxonomy) and then aggregated to a single, usually weighted, mean. In both cases, i.e. primitive value domains and object sets, the result of the field-level dissimilarity function is real number between 0 and 1.
The above computation clearly requires the presence of at least one meaningful taxonomy over the concerned concept. In some cases, however, it is impossible to ensure the availability of classes, especially when the whole process is aimed at class discovery. Therefore, the comparison of objects remains only possible with respect to their field values. In such cases, T-TREE applies the same dissimilarity function as on initial objects, i.e. a weighted City block distance. It also applies clustering in order to better characterise the domains of the fields of the initial concept.
A technique of this kind may lead, when some circuits in object definitions occur, to a deadlock between dissimilarity computation tasks. In fact, it may happen that the dissimilarity of a pair of objects depends on the dissimilarity of another pair which in turn depends on the first dissimilarity. In such a case, a fixed point computation is applied in order to simultaneously evaluate the proximity of all mutually dependant pairs. The definitions of the dissimilarity on each pair is used to extract characterization functions which further compose a system of equations. The underlying vector function is repeatedly applied on an initial solution until a suitable approximation of the function fixed point is obtained. Its components represent approximations of the dissimilarities saught.

Clustering algorithms

Several algorithms of the Sequential Agglomerative Hierarchical Non-overlapping familly are currently available (complete, single -- a.k.a. nearest neighbours --, average linkage). They can be characterised as ascending binary clustering algorithms (which progressively aggregate classes, starting from the instances, and only aggregate two classes in a row). The algorithms begin by considering each object as a class. Then, at each step, they aggregate into a new class the two classes which contains the nearest objects with regard to the dissimilarity measure. This new class contains the objects of the two previous ones which are not considered further. The algorithm stops when there is only one class left.
Based on the above values, a clustering algorithm will try to divide the set of objects into homogeneous sub-sets. I.e., object groups will be looked for such that the member objects score to low values of the pairwise dissimilarity whereas the pairs of objects in different groups score to higher values. In the example, a sub-group will be created including house-1 and house-2 since their dissimilarity, 0.376, is substantially lower than the one of the pairs ( house-1, house-3) and ( house-2, house-3). Thus two classes will be generated c1 and c2, having extensions { house-1, house-2, house-3} and { house-1, house-2} respectively. In other terms, c2 is a sub-class of c1.

Generalisation

The result of the clustering phase is an inclusive hierarchy of sets of objects. In order to provide a description corresponding to these sets, a class description is inferred from each set of objects provided. The details of the generalisation mechanism provided are not described here. However, the application of the generalisation procedure on above example yields the following partial class descriptions: 
<c1
	fields = {
		<address domain = {"eybens", "grenoble"};>,
		<number intervals = {[13 113]};>,
		<floor intervals = {[0 4]};>};>
<c2
	superclass = c1;
	fields = {
		<address domain = {"grenoble"};>,
		<number intervals = {[21 113]};>,
		<floor intervals = {[0 2]};>};>

Interface

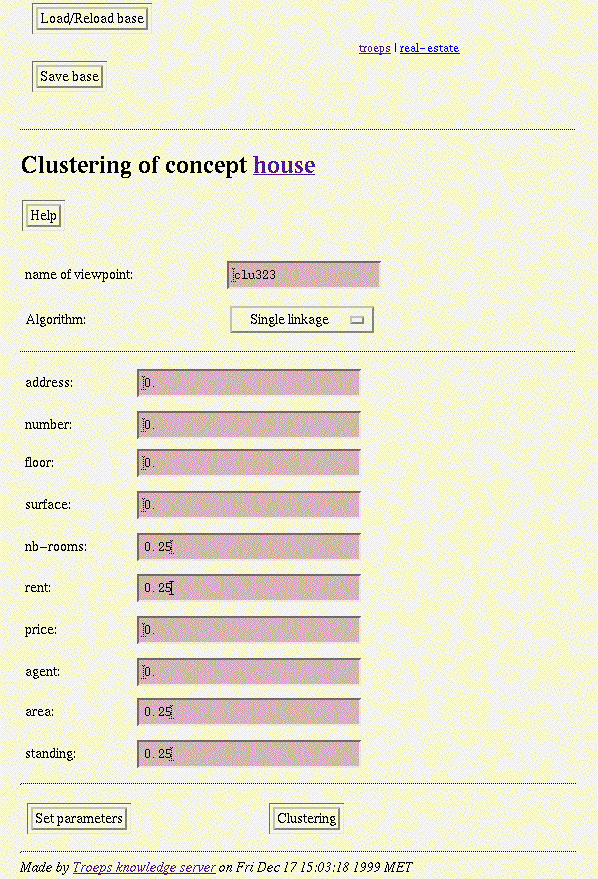
Screendump 48: Clustering initialisation.

Screendump 49: Object dissimilarity completion.

Screendump 50: Clustering result.

Screendump 51: Dissimilarity initialisation.

Screendump 52: Dissimilarity result.

API

(tr-clustering concept method create-p viewname slots ) function in [libtrt]

-> (), concept concept nak,method string nas, create-p boolean, viewname string nas,adkv , slots ( (conceptslot naks . float bcf) nal *) nal
Builds a new taxonomy of classes for concept concept in a viewpoint called viewname (which is created if create-p is not ()) by considering only the slots in slots with their respective weight comprised between 0. and 1.. The method used for clustering depends on the first element of the method argument (available methods are "mv", "al", "sl" and "cl"). This API function works perfectly for fields whose type is not another concept. In the opposite event, each such classslot must be created and the clview annotation set to the name of the concept view (of the domain concept) to use. This view must have been created. Either, it already has a taxonomy which is then used or it has class fields in its root class whose clweight annotation is set to a weight and clalgo whose value is the name of an algorithm as above and this recursively.
(tr-find-slot-similar object slots) function in [libtrt]

-> ((object . float)*), object object nao, slots ( (conceptslot naks . float bcf) nal *) nal
Compare the object object with all the other instances of its concept on the basis of the set slots of fields weighted by floats between 0. and 1. (whose sum is 1.) and returns their list ordered by higher similarity. This uses the weighted agglomeration of the dissimilarity between the concerned field values.
(tr-find-view-similar object views) function in [libtrt]

-> ((object . float)*), object object nao, views ( (conceptview nakv . float bcf) nal *) nal
Compare the object object with all the other instances of its concept on the basis of the set views of views weighted by floats between 0. and 1. (whose sum is 1.) and returns their list ordered by higher similarity. This uses the weighted topological dissimilarity over the concerned views.

Examples

Bridge inference

Once taxonomies have been built and objects have been attached, it is very convenient to be able to compare them. To that extent, bridge inference algorithms are provided which produce bridges holding between the classes of the taxonomies.
The algorithms are used from a set of classes and a class and they look for all the bridges which involve subclasses of the former as source and subclasses of the latter as destination. The algorithms compare the classes and if all the "conjunction" of the source classes is smaller than the destination classes. However, it only returns the minimal bridges in the meaning provided in the Bridge section. So, the user can choose to implement a non minimal bridge. But any bridge not covered by a bridge returned by the algorithm is not valid.
There are two versions of the algorithm depending on the predicates they rely on. A first version uses the members of the classes such that conjunction is intersection of these member sets and comparison is inclusion; the second version uses the types of the classes such that conjunction is type intersection and comparison is a sub-typing test.

Interface

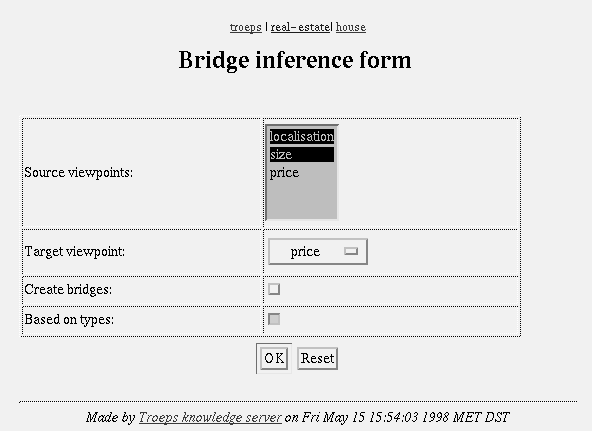
Screendump 53: Bridge inference initialisation.

Screendump 54: Bridge inference result.

API

( tr-find-bridges-from-objects classes class create-p ) function in [libtrt]

-> { ( (class*) . class)* }, classes class nas,class class nac,ivc, create-p boolean
Looks for all the minimal possible bridges which have a subset of subclasses of classes as source and a subclass of class as destination. The possibility of a bridge is judged with regard to the set of objects members of each class. The bridges are created if create-p evaluates to true, their compositions are returned otherwise.
(tr-find-bridges-from-types classes class create-p ) function in [libtrt]

-> { ( (class*) . class)* }, classes class nas,class class nac,ivc, create-p boolean
Looks for all the minimal possible bridges which have a subset of subclasses of classes as source and a subclass of class as destination. The possibility of a bridge is judged with regard to the type of each class. The bridges are created if create-p evaluates to true, their compositions are returned otherwise.

Examples

Complete example

Let the set of objects be the one contained in the real-estate knowledge base provided in the example directory. The set of 10 objets is given below with the relevant slot values:

#
address
number
floor
area
standing
nb-rooms
rent
1
factory St
17
3
grenoble
fair
4
6000.
2
meylan
176
3
meylan
fair
3
8000.
3
smh
95
3
smh
low
1
3000.
4
grenoble
113
0
grenoble
low
2
4000.
5
meylan
60
6
meylan
high
4
11000.
6
eybens
47
0
eybens
fair
2
7000.
7
eybens
13
4
eybens
fair
8
11000.
8
grenoble
21
2
grenoble
low
3
8000.
9
grenoble
32
3
grenoble
high
5
14000.
10
rue Monge
3
2
paris
fair
2
15000.

These object are first classified and attached to the most non ambiguous specialised class (i.e. the lowest class to which the objects can be attached while they cannot be attached to a non comparable class). For instance, the house #4 is attached to other-area while it can be attached to both industrial and residential. The result is given in the table below and in Figure 12 . It is noteworthy that object 5, 9 and 10 are not attached to high under the price viewpoint because of a bridge stating that the high priced houses are palaces (that which these houses cannot pretend to be since they have at most 3 rooms). On the contrary, house #7 is attached to high because it can be attached to palace.

#
localisation
size
price
new
1
center
More than 3
average
t3-5
2
suburbs
T3
average
t3-5
3
suburbs
H
low
t3-10
4
other-area
T2
low
t3-10
5
suburbs
More than 3
house
t3-9
6
suburbs
T2
average
t3-5
7
suburbs
Palace
high
t3-5
8
other-area
T3
average
t3-10
9
center
More than 3
house
t3-9
10
center
T2
house
t3-5

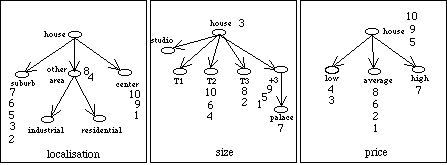
Figure 12: The various viewpoints and the attached objects after classification.
A new viewpoint is created by clustering on the slots area, standing, nb-rooms and rent with the same .25 weight. Interesting resulting classes are provided in Figure 16 . It retains only the upper classes (the other ones have been discarded -- that which, as like as renaming classes, is easily done with the graphic user interface). It can be noted that only one field ( standing) allows to discriminate the classes. This is due to the importance of the dissimilarity between different nominal values. Overall, the classes t3-10 and t3-9 corresponds to two homogeneous groups (they can be independently discriminated by the standing, rent and nb-rooms fields.

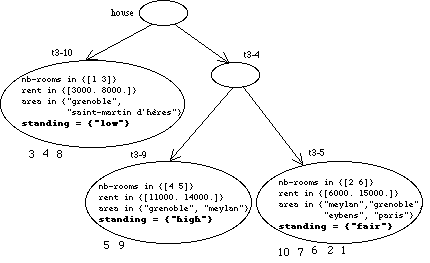
Figure 13: Interesting classes in the new viewpoint.
Last, it is possible to call the bridge inference methods in order to investigate the correlation between classes of different viewpoints. Figure 14 displays the result when using the inference from objects between viewpoints size, price and the newly created viewpoint.

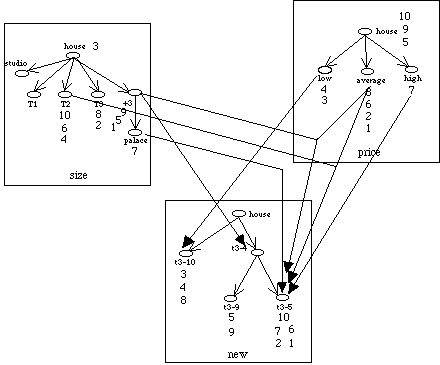
Figure 14: Bridge inference based on objects. Here are all the maximal bridges which do not target the root class.