Data
model
Knowledge
representation aims at representing a particular domain and reasoning about it.
This is what
TROEPS
is about.
A
knowledge
base is the repository for the pieces of knowledge on a domain. It can also use
other knowledge bases and resources. It is made of four kinds of knowledge:
- Descriptive
knowledge is represented in an object-based knowledge representation system.
This enables the representation of classes of objects (e.g. house), subclasses
(e.g. palace) and the identification of an object as belonging to such a class.
It provides constraint satisfaction and typing mechanisms for the objects.
- Methodological
knowledge specifies the ways to select and link up methods for a given task. It
is represented through a task management system able to integrate, represent,
process and monitor computer programs.
- Behavioural
knowledge concerns the modelling of dynamic phenomena, such as the dynamics of
contract negotiation between buyers and sellers, through a qualitative
modelling system.
- Textual
annotations
on the various objects and tasks involved are achieved through a hypertext
system which connects hypertext nodes with the components of the descriptive
and methodological knowledge. It allows browsing among texts, objects and
tasks. Here textual annotations are not part of the
TROEPS
model: in
TROEPS,
the language for expressing them is the
HTML
standard.
In
the current state of
TROEPS,
only the first and last part are available and described in the manual.
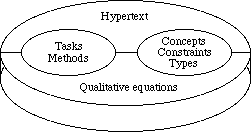
Figure
1: The four parts of a knowledge base.
TROEPS
is an object-based knowledge representation model. This means that individuals
are represented as objects. These objects are partitioned in concepts (an
object is instance of one and only one concept). An object is thus an instance
of a concept; it is attributed a set of fields which are described in the
concept. A field expresses either a property, a "part-of" relation link, or a
relational link. Fields thus allow to express the relationship between objects
(and concepts). The different perspectives one can have on an object are
represented through viewpoints: a viewpoint determines first the set of fields
which are relevant (or visible) and a hierarchy of classes in which the
instances of the concept can be classified under that viewpoint. Classes
introduce constraints on the field values of objects which are member of them.
They are related through the specialisation relation which determines
progressive subsets of the set of the instances of the concept (see
Figure
2
).
This progression is supported by the progression of the constraints added from
specialisations to the classes they specialise. In each viewpoint, an object is
attached to only one class, but is a member of all the classes of which this
class is a specialisation. Class taxonomies are the support of powerful
classification mechanisms described in the third section. Viewpoints allow one
to focus only on the relevant aspects of objects while hiding those which are
not. A bridge can be thrown from a set of classes (called the source) to
another class (called the destination) of different viewpoints in a concept in
order to signify that the instances which are member of all the source classes
are also member of the destination class.
For
instance, if the domain to be modelled is that of a real estate agency, three
viewpoints can be put forth for the
house
concept. These viewpoints cover the topics of
localisation,
size
and
price
on the
house
concept. The
localisation
viewpoint distinguishes
center
apartments,
suburban
houses and
other-area
among which
residential
and
industrial
places. The
size
viewpoint differentiates flats by the number of their rooms (usually normalised
as
studio,
F1,
F2,
F3...
palace).
Lastly, from the
price
viewpoint there are three rent categories:
low,
average
and
high
price.
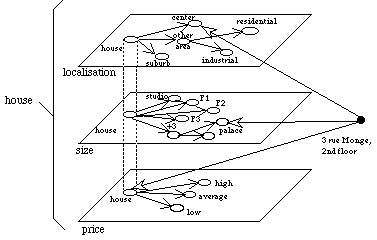
Figure
2: The
house
concept in the
real-estate
knowledge base.
The
present chapter explores the different entities that are to be understood in
order to describe objects in a knowledge base. It does this by going from the
more general notion (knowledge base) to the more specific (object). However the
reader should keep in mind the headlines drawn above in order to get
familiarised with each notion presented here. A glossary, in Appendix
9,
can help to remind some specific notions.
Interface
Screendump
1:
TROEPS
server home page.
API
- (tr-init) function
in [libtrp]
->
boolean
- Initialises
the
TROEPS
system by defining the primitive notions which are described hereafter. Calling
this function is compulsory before any use of
TROEPS.
It can be used in order to re-initialise the whole system: then, any
user-defined notion or loaded knowledge base is discarded from the environment.
- (tr-version) function
in [libtrp]
->
(integer*)
- Prints
the version number and returns a list of integers denoting the current version
of the system.
Examples
$ italk
;;; ILOG Talk version 3.3 [sparc_5_gnu]
;;; Copyright (c) 1989-1997 by ILOG
;;; Write to talk-support@ilog.com for help
;;; Image saved on Fri Jul 4 19:26:59 1997
;;; Connecting to Emacs server...connected.
;;; Loading workspace 'talk': Ilog Talk kernel workspace
;;; Loading workspace 'trp': Troeps development workspace
;;; Loading workspace 'trt': Troeps taxonomy building tool workspace
;;; Loading workspace 'htrp': Troeps knowledge server development workspace
;;; Loading workspace 'divers': executables and utility files workspace
;;; Welcome to ILOG Talk.
;;; Type (exit) to leave Talk.
? (load-program-unit 'libtrl)
;;; Loading library 'libtrl': Troeps textual interface
;;; Loading run-time environment of 'libtrl': (libtrp)
;;; Loading library 'libtrp': The core Troeps library
;;; Loading object file "/home/lotse/sherpa/TROPES.0/src/sparc_5_gnu/lib/libtrp.so"
;;; Loading object file "/home/lotse/sherpa/TROPES.0/src/sparc_5_gnu/lib/libtrl.so"
= libtrl
? (load-program-unit 'trtdum)
;;; Loading module 'trtdum': Troeps dummy basic type descriptions
;;; Loading object file "/home/lotse/sherpa/TROPES.0/src/sparc_5_gnu/o/trtdum.o"
= trtdum
? (tr-version)
;;; Troeps 1.3a, (C) INRIA, 1992-1999
= (1 3 . 1)
? (add-handler (function troeps-handler))
= #<handler-function troeps-handler #p0019ad70>
? (tr-init)
= t
? (exit)
$
Knowledge
base
A
knowledge
base
groups a set of descriptions concerning the entities occurring in a particular
domain. It thus contains a set of concepts (together with their viewpoints,
fields, classes, objects and bridges) and a set of knowledge base viewpoints
(see below). However, in order to be linked with other domain descriptions, the
knowledge base contains reference to a set of other components:
- the
name of the file in which the knowledge base is stored;
- the
other knowledge bases it imports (this is useful, for instance if the concepts
in the base refer to other concepts);
- the
set of abstract data types (see Appendix
5)
used in the base;
- the
set of object files for the knowledge base (for efficiency purpose, they will
be disconnected from the knowledge base scheme, thus enabling to be connected
to a secondary storage manager);
- the
set of
TALK
modules to be included in the knowledge base (since some programs for
manipulating the knowledge could be useful);
For
the time being, a knowledge base can be created and manipulated. It can also be
set as current so that each newly created concept will be considered as
belonging to that base and will be saved with the base. It can also be loaded
from and saved on files of various formats which are explained in Appendix
2.
Concerning
data types, the knowledge base loader is not able to load type descriptions
thus, they must be loaded independently of the knowledge bases.
TROEPS
is currently provided with a type module (
trtdum)
which declares base types (see Appendix
3).
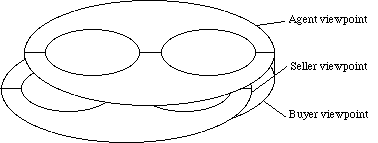
Figure
3: The
real-estate
knowledge base can be used by several people. Then, it can be seen from several
viewpoints:
agent,
seller,
buyer
(for instance).
Knowledge
base viewpoints
A
knowledge base aims at modelling and structuring knowledge. This knowledge may
come from different (sub-)domains on one hand, and the users may, on the other
hand, consider their own set of knowledge, of properties and relations between
pieces of knowledge. So, knowledge has to be organised in such a way that
viewpoints may be described.
TROEPS
includes the
viewpoint
notion. Viewpoints have been designed in order to allow specialists in
different domains to express their knowledge independently of one another. A
viewpoint represents a specific point of view on the knowledge included in the
knowledge base. Viewpoints are described at the upper level in the knowledge
base and can then be viewpoints on the concepts described in the knowledge base.
These
global viewpoints on the knowledge base do not have special prerogatives in the
current implementation (they are presented for completeness purposes). They
must be distinguished from the concept viewpoints which will be presented later
on.
Interface
Screendump
2: Knowledge base display.
Screendump
3: Knowledge base edition.

Screendump
4: Knowledge base statistics.
API
- (tr-base-p
anything) predicate
in [libtrp]
-> boolean,
anything
entity
- Returns
anything
if the argument
anything
is a knowledge base,
()
otherwise.
- (tr-create-base
basename
optional: filename
) function
in [libtrp]
-> base,
basename
string
nas,adb,
filename
filename
fnf
- Creates
and returns a new knowledge base of name
basename.
It will therefore be known of the system until deletion or initialisation.
- (tr-find-base
basename) function
in [libtrp]
-> base,
basename
string
nas
- Retrieves
and returns the knowledge base of name
basename.
When no such base is known, returns
().
- (tr-base
basename) macro
in [libtrp]
-> base,
basename
string
nas
- Retrieves
and returns the knowledge base of name
basename.
When no such base is known, creates and returns it.
- (tr-delete-base
base) function
in [libtrp]
-> boolean,
base
base
nab,
neo
- Deletes
the knowledge base
base
from the environment. This can only happen if the knowledge base is as empty as
at its creation. Afterwards, the knowledge base does not exist anymore in the
environment.
- (tr-erase-base
base) function
in [libtrp]
-> boolean,
base
base
nab,
neo
- Deletes
the knowledge base
base
and its content from the environment. Afterwards, neither the knowledge base
nor the concepts and objects refered by it exist anymore in the environment.
- (tr-base-name
base) function
in [libtrp]
-> string,
base
base
nab
- Returns
the name of the knowledge base
base.
- (tr-base-rename
base
name
) function
in [libtrp]
-> string,
base
base
nab,
name
string
nas,
adb
- Changes
the name of the knowledge base
base
for the string
name.
- (tr-base-filename
base) setfable
function in [libtrp]
-> filename,
base
base
nab
- Returns
the filename of the knowledge base
base.
Can be used for changing that filename.
- (tr-add-viewpoint
base
viewpointname) function
in [libtrp]
-> boolean,
base
base
nab,
viewpointname
string
nas
- Adds
the viewpoint name
viewpointname
to the set of viewpoints of the base
base.
- (tr-rem-viewpoint
base
viewpointname) function
in [libtrp]
-> boolean,
base
base
nab,
viewpointname
string
nas,nib
- Removes
the viewpoint name
viewpointname
from the set of viewpoints of the base
base.
- (tr-base-viewpoints
base) function
in [libtrp]
-> { string* },
base
base
nab
- Returns
the set of viewpoint names of the base
base.
- (tr-add-concept
base
concept) function
in [libtrp]
-> boolean,
base
base
nab,
concept
concept
nak
- Adds
the concept
concept
to the set of concepts of the base
base.
- (tr-rem-concept
base
concept) function
in [libtrp]
-> boolean,
base
base
nab,
concept
concept
nak,nib
- Removes
the concept
concept
from the set of concepts of the base
base.
- (tr-base-concepts
base) function
in [libtrp]
-> { concept* },
base
base
nab
- Returns
the set of concepts of the base
base.
- (tr-base-sorted-concepts
base
optional: sort-function
) function
in [libtrp]
-> { concept* },
base
base
nab,
sort-function
function
- Returns
the set of concepts of the base
base
in their creation order or the order of the base description file by default.
If the
sort-function
is provided, the concepts are sorted according to it.
- (tr-add-import
base
base2) function
in [libtrp]
-> boolean,
base
base
nab,
base2
base
nak
- Adds
the base
base2
to the set of imported bases of the base
base.
- (tr-rem-import
base
base2) function
in [libtrp]
-> boolean,
base
base
nab,
base2
base
nak,nib
- Removes
the base
base
from the set of imported bases of the base
base.
- (tr-base-imports
base) function
in [libtrp]
-> { base* },
base
base
nab
- Returns
the set of imported bases of the base
base.
- (tr-add-type
base
type) function
in [libtrp]
-> boolean,
base
base
nab,
type
type
nak
- Adds
the type
type
to the set of types of the base
base.
- (tr-rem-type
base
type) function
in [libtrp]
-> boolean,
base
base
nab,
type
type
nak,nib
- Removes
the type
type
from the set of types of the base
base.
- (tr-base-types
base) function
in [libtrp]
-> { type* },
base
base
nab
- Returns
the set of types of the base
base.
- (tr-add-instance-file
base
filename) function
in [libtrp]
-> boolean,
base
base
nab,
filename
string
nas
- Adds
the instance file
filename
to the set of instance files of the base
base.
- (tr-rem-instance-file
base
filename) function
in [libtrp]
-> boolean,
base
base
nab,
filename
string
nas,nib
- Removes
the instance file
filename
from the set of instance files of the base
base.
- (tr-base-instance-files
base) function
in [libtrp]
-> { string* },
base
base
nab
- Returns
the set of instance files of the base
base.
- (tr-add-lexicon
base
filename) function
in [libtrp]
-> boolean,
base
base
nab,
filename
string
nas
- Adds
the lexicon file
filename
to the set of lexicons of the base
base.
- (tr-rem-lexicon
base
filename) function
in [libtrp]
-> boolean,
base
base
nab,
filename
string
nas,nib
- Removes
the lexicon file
filename
from the set of lexicons of the base
base.
- (tr-base-lexicons
base) function
in [libtrp]
-> { string* },
base
base
nab
- Returns
the set of lexicons of the base
base.
- (tr-add-module
base
modulename) function
in [libtrp]
-> boolean,
base
base
nab,
modulename
string
nas
- Adds
the module name
modulename
to the set of
TALK
modules of the base
base.
- (tr-rem-module
base
modulename) function
in [libtrp]
-> boolean,
base
base
nab,
modulename
string
nas,nib
- Removes
the module name
modulename
from the set of
TALK
modules of the base
base.
- (tr-base-modules
base) function
in [libtrp]
-> { modulename* },
base
base
nab
- Returns
the set of
TALK
modules of the base
base.
- (tr-current-base) setfable
function in [libtrp]
-> base,
base
base
nab
- Returns
the current knowledge base. Can be modified by the form:
(setf
(tr-current-base) base)
.
- (tr-print-report
base) function
in [libtrp]
-> (),
base
base
nab
- Prints
a statistical report on the number of entities in the base
base.
Examples
? (setf (tr-current-base) (tr-create-base "my-real-estate" #f"my-real-estate.bdf"))
= (tr-base "my-real-estate")
? (tr-base-p ())
= ()
? (tr-base-p (tr-current-base))
= (tr-base "my-real-estate")
? (eq (tr-current-base) (tr-find-base "my-real-estate"))
= t
? (tr-base "my-real-estate")
= (tr-base "my-real-estate")
? (tr-delete-base (tr-base "my-real-estate"))
= t
? (tr-load-base #f"examples/real-estate.bdf")
= t
? (tr-base-name (tr-current-base))
= "real-estate"
? (tr-base-viewpoints (tr-current-base))
= ("localisation" "size" "price" "function" "test")
? (tr-base-concepts (tr-current-base))
= ((tr-concept "house") (tr-concept "room") (tr-concept "human"))
? (tr-base-sorted-concepts (tr-current-base))
= ((tr-concept "human") (tr-concept "room") (tr-concept "house"))
? (tr-print-report (tr-current-base))
Statistics on the base: real-estate
external types: 0
concepts: 3
conceptslots: 20
conceptviews: 5
classes: 29
filters: 0
classslots: 34
objects: 10
house: 9
room: 0
human: 1
= ()
? (tr-base-filename (tr-current-base))
= #f"examples/real-estate.bdf"
? (tr-erase-base (tr-current-base))
= t
? (tr-load-base #f"examples/real-estate.bdf")
= t
? (setf (tr-current-base)
(tr-create-base "my-real-estate" #f"my-real-estate.bdf"))
= (tr-base "my-real-estate")
? (tr-add-import (tr-current-base)
(tr-find-base "real-estate"))
= ((tr-base "real-estate"))
? (tr-base-imports (tr-current-base))
= ((tr-base "real-estate"))
? (tr-base-imports (tr-find-base "real-estate"))
= ()
Concepts
Partition
of a knowledge base
A
knowledge base may distinguish between different and disjoint sets of objects.
Let us consider, for instance, the real estate base; it includes families as
different as
human,
house
and
room.
In
TROEPS,
such a family is called a
concept.
In a knowledge base, concepts define a partition of the universe: any
individual object is instance of one and only one concept.
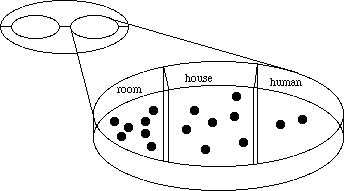
Figure
4: The partition of the
real-estate
knowledge base into several concepts:
room,
house
and
human.
Structure
of concept instances
Individuals,
in a concept, are described by their fields; the same fields and only these
fields are used to describe the instances of a concept. For instance, the
house
concept defines the field
address,
surface,
floor,
etc. So, the concept is the working space for field names: they are known of
the whole concept and, thus, the occurrence of the same field name in the same
concept refer to the same field. For instance, the field
age
in the
house
concept represents the age of the building in which the apartment is. But, on
another hand, two different fields in two different concepts can have the same
name (for instance, the
human
concept can have an
age
field too).
These
fields are defined at the concept level. The mandatory field definition
describes the whole information valid for any occurrence of it in the concept.
It includes:
- the
general field type,
- its
nature (property, component or relation),
- the
constructor, to distinguish sets, lists or atomic values,
- and
the tree of methods available to calculate the field value.
These
notions are detailed in the "concept field" section.
Identity
and integrity
The
objects are identified within a concept through a key. This means that, in each
concept, a set of fields (called the key) is distinguished. Any instance of the
concept is identified by the value of these fields. For instance, the
identification of a person can be done by the "social security number" or
her/his full name and birthday; an apartment is identified in a unique manner
by the set of fields:
{address,
floor, number}
;
a "real estate agent" can be defined by its name and the name of its
"subsidiary". So, there do not exist two instances with the same values for all
the key-fields. Not only the key is unique (which warrants identity) but it is
invariant (which warrants integrity): one cannot change what makes the identity
of an object. All these properties are ensured by the
TROEPS
system. Another constraint on the key is that it must be visible under any
viewpoint in order to identify the object.
Furthermore,
TROEPS
allows to handle incomplete instances, but the values of key fields is the
minimal information required to create an object and manipulate it. In such a
way, the system considers this object as a member of a concept in the knowledge
base, so it may identify it as different from other instances.
TROEPS
does not handle multiple keys on objects: for instance, an estate agent,
usually retrieves the houses from their price and number of rooms rather than
from their location. It could be convenient to address the same set of objects
by both keys, but
TROEPS
does not offer it (however, this can be easily added if necessary; but multiple
keys would introduce unavoidable functional dependencies which would have to be
taken into account by the implementation).
Thus,
minimal information for an instance is the name of the concept plus the set of
valued fields of the key.
Keys
and cycles
The
dependency graph between keys (i.e. the graph which links a concept to the
concepts which are the type of its key fields) cannot contain cycles. This is
motivated by both computational and semantic considerations. For the latter, if
it is required for an object to have a defined key in order to exist, then this
key must refer to an existing object which does not depend upon the given
object. Thus, circularities must be prohibited at the level of the object keys.
One could imagine circularities at the concept level which do not imply
circularities for the objects. For instance, one can give as the key of the
human
concept the fields
father,
mother
and
surname
with
father
and
mother
being
human.
This makes sense but can only be interpreted upon an infinite domain of human
beings.
TROEPS
prohibits such kind of non-circular key reference at the instance level which
leads to circular reference at the concept level, because it is harmful for the
user. As a matter of fact, this raises problems because for creating your first
human you must provide his (or her) parents which are also humans. Tackling
interpretation over infinite domains of objects could be the subject of a
further version of
TROEPS
introducing the lazy instanciation of keys.
As
a consequence of non circularity through keys, concepts can be partially
ordered and this order must be respected by the knowledge base file format (see
Appendix
2).
In
this first version of
TROEPS,
it is also not possible to have circularities through any kind of slots. This
must change soon, but for the time being it is possible to use links (see
conceptslot) instead of first class concept slots.
Reference
Concepts
are not totally independent, however. Even if concepts are different, they are
related in some manner in the universe to be modelled. In
TROEPS,
this interaction is modelled through the fields and components of the concept
instances. For instance, in the
house
concept
,
the field
inhabitant
has its values in the concept
human.
In
this first version of
TROEPS,
it is not possible to refer to a previously undefined concept in a concept.
This will be changed soon.
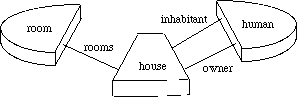

Figure
5: The fields
inhabitant
and
owner
(resp.
rooms)
in the
house
concept has instances of the concept
human
(resp.
room)
as values (upper drawing). Also depicted in an entity relationship diagram
(lower one).
The
nature of the reference is modelled through the nature descriptor of the
concept field.
Visibility
versus typing
The
restrictions introduced by the use of viewpoints are manifold. One can
distinguish between the hiding of properties and definition of properties. A
viewpoint only introduces the hiding of properties: when some fields are not
reachable under a particular viewpoint, this does not mean that objects do not
have these fields but that they are not visible from the viewpoint. However,
objects do have these fields. As a consequence, even if the fields are not
visible, they can still introduce some constraints on the object (imagine a
magnet, you cannot see the polarity but there are positions in which it cannot
remain). This could lead to some surprise for the programmer: the hidden parts
of an object still play their role in the shadow. This is mainly relevant for
concepts in which there are a lot of bridges and inter-field constraints.
Also,
this is related with the definition of field types. When it is said that the
type descriptor of a class field can have a set of classes (of different
viewpoints) as values, this has to be interpreted as a constraint but not as a
visibility information: the constraint is that the value of the field (in order
for the object to be in the class) must be member of each of the classes. It
does not mean that the value is only visible under the corresponding viewpoints.
Interface

Screendump
5: Concept display.
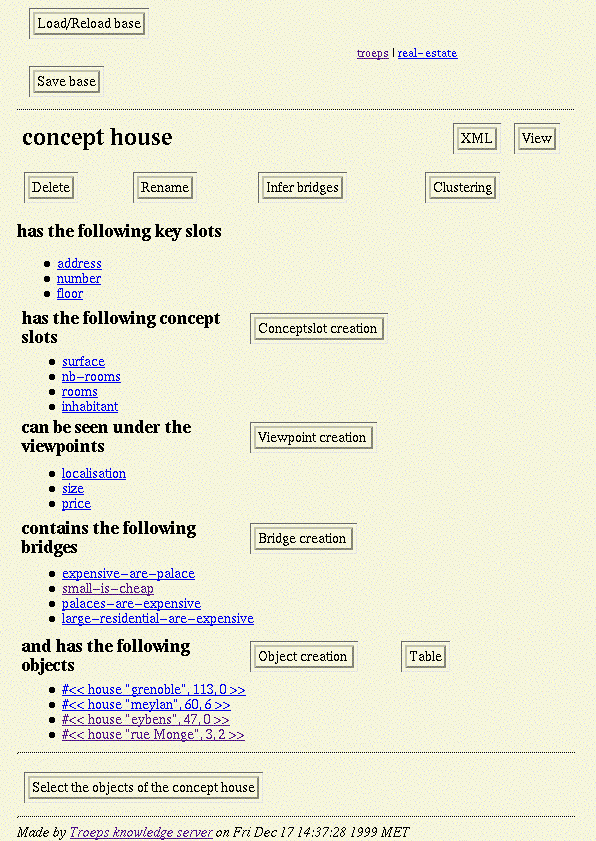
Screendump
6: Concept edition.

Screendump
7: Concept creation.
API
- (tr-concept-p
anything) predicate
in [libtrp]
-> boolean,
anything
entity
- Returns
anything
if the argument
anything
is a concept,
()
otherwise.
- (tr-create-concept
conceptname
key) function
in [libtrp]
-> concept,
conceptname
string
nas,adk,
key
( (
name
string
nas
type
string|concept
ivt
constructor string
nas,ivc
nature string
nas,ivn)ivks+
)
ivks,
esk
- Creates
and returns a new concept of name
conceptname
and the provided set of concept fields specifications (
key)
as key. It will therefore be known of the system until deletion or
initialisation.
- (tr-find-concept
conceptname) function
in [libtrp]
-> concept,
conceptname
string
nas
- Retrieves
and returns the concept of name
conceptname.
When no such concept is known, returns
().
- (tr-concept
conceptname
key
) macro
in [libtrp]
-> concept,
conceptname
string
nas,
key
( (
name
string
nas
type
string|concept
ivt
constructor string
nas,ivc
nature string
nas,ivn)ivks+
)
ivks,
esk
- Retrieves
and returns the concept of name
conceptname.
When no such concept is known, creates it (with the key specification
key)
and returns it.
- (tr-delete-concept
concept) function
in [libtrp]
-> boolean,
concept
concept
nak,
neo
- Deletes
the concept
concept
from the environment. This can only happen if the concept is as empty as at its
creation. Afterwards, the concept does not exist anymore in the environment.
- (tr-erase-concept
concept) function
in [libtrp]
-> boolean,
concept
concept
nak,
neo
- Deletes
the concept
concept
and its content from the environment. Afterwards, neither the concept nor the
conceptviews, conceptslots, bridges and objects it contains exist anymore in
the environment.
- (tr-concept-name
concept) function
in [libtrp]
-> string,
concept
concept
nak
- Returns
the name of the concept
concept.
- (tr-concept-rename
concept
name
) function
in [libtrp]
-> string,
concept
concept
nak,
name
string
nas,
adk
- Changes
the name of the concept
concept
for the string
name.
This also changes the names of the root classes of each concept viewpoint if any.
- (tr-concept-key
concept) function
in [libtrp]
-> ( keyslot* ),
concept
concept
nak
- Returns
the key of the concept
concept,
i.e. the (ordered) list of keyslots which forms the key.
Known
bug: this is currently a set of string (the names of the key slots) which is
returned.
- (tr-concept-slots
concept) function
in [libtrp]
-> { conceptslot* },
concept
concept
nak
- Returns
the set of concept slots of the concept
concept.
- (tr-concept-sorted-slots
concept
optional: sort-function
) function
in [libtrp]
-> { conceptslot* },
concept
concept
nak,
sort-function
function
- Returns
the set of concept slots of the concept
concept
in their creation order or in their order in the base description file by
default. If the
sort-function
is provided, the concept slots are sorted according to it.
- (tr-concept-views
concept) function
in [libtrp]
-> { conceptview* },
concept
concept
nak
- Returns
the set of concept views of the concept
concept.
- (tr-concept-sorted-views
concept
optional: sort-function
) function
in [libtrp]
-> { conceptview* },
concept
concept
nak,
sort-function
function
- Returns
the set of concept views of the concept
concept
in
their creation order or in their order in the base description file by default.
If the
sort-function
is provided, the concept views are sorted according to it.
- (tr-concept-bridges
concept) function
in [libtrp]
-> { bridge* },
concept
concept
nak
- Returns
the set of bridges across viewpoints of the concept
concept.
- (tr-concept-instances
concept) function
in [libtrp]
-> { instance* },
concept
concept
nak
- Returns
the set of instances of the concept
concept.
- (tr-concept-sorted-instances
concept
optional: sort-function
) function
in [libtrp]
-> { instance* },
concept
concept
nak,
sort-function
function
- Returns
the set of instances of the concept
concept
in
their creation order or in their order in the base description file by default.
If the
sort-function
is provided, the objects are sorted according to it.
Examples
? (tr-create-concept "agent"
'(("name" "chaine" "un" "propriete"))
("subsidiary" "chaine" "un" "propriete")))
= (tr-concept "agent")
? (tr-find-concept "agent")
= (tr-concept "agent")
? (tr-concept-p (tr-find-concept "agent"))
= (tr-concept "agent")
? (tr-delete-concept (tr-concept "agent"))
= t
? (tr-concept-p ())
= ()
? (tr-create-concept "agent" '(("name" "chaine" "un" "propriete")))
= (tr-concept "agent")
? (tr-add-concept (tr-current-base) (tr-find-concept "agent"))
= ((tr-concept "agent"))
? (tr-base-concepts (tr-current-base))
= ((tr-concept "agent"))
? (tr-concept-name (tr-find-concept "agent"))
= "agent"
? (tr-concept-key (tr-find-concept "agent"))
= ("name")
? (tr-concept-slots (tr-find-concept "agent"))
= ((tr-conceptslot (tr-concept "agent") "name"))
? (tr-concept-views (tr-find-concept "agent"))
= ()
? (tr-concept-views (tr-find-concept "agent"))
? (tr-concept-bridges (tr-find-concept "agent"))
= ()
? (tr-concept-instances (tr-find-concept "agent"))
= ()
? (tr-concept-instances (tr-find-concept "agent"))
= ()
Field
definition: conceptual aspects
Field
definitions assert that the instances of a concept have a particular set of
fields. They also assert important characteristics of the fields such as the
type of the field value, the fact that it is a property or a composition link.
They thus define the structure of the objects. The definition of a concept
field is unique for the whole concept. It contains the minimum information for
TROEPS
to handle the field values of individual objects. It is valid under each
viewpoint in which it can only be refined. The definition of a concept field
appears in the definition of the concepts; for a field to appear in a class, it
must have been defined in the concept first; conversely, a field can appear in
a concept and remain hidden under every viewpoint. It is thus useless for
manipulation by the user of the knowledge base but participates in the essence
of the concept. The characteristics of the concept field are:
- The
base type of the values of the fields;
- The
constructor of the type if necessary;
- The
nature of the field;
- Computation
mechanisms.
Each
of these characteristics are introduced by what is called a descriptor. As an
example the
size
field of a
house
is a property (
propriete
nature), has only one (
un
constructor) value which is an
integer
(type) and can be computed by summing the size of the
rooms
field which is a composite (
component
nature) field whose value is a set (
ensemble
constructor) of objects in the
room
concept (type). All is detailed below.
Type
The
type descriptor for a concept introduces the basic value type of a particular
field. There are two important kinds of field values in
TROEPS:
objects (instances of a
TROEPS
concept) and values (of a particular basic type). In addition, the field value
itself can be a homogeneous collection of objects or values. This is indicated
by the constructor descriptor (see below). When the basic value must be an
object, the value of the type descriptor is the concept to which that object
must belong. When it is a value, the value of the type descriptor must be the
type of the value. Types must be distinguished between elementary types and
record types.
Elementary
types are defined in the type system through abstract data types.
TROEPS
is provided with a basic set of types (
entier,
chaine,
booleen,
reel)
through the
trtdum
module. The user can extend this set very easily (see Appendix
5).
Record
types are automatically created by the type system in order to help many tasks
of the
TROEPS
system. They are accessible as types by the user. Thus, it is possible to
declare a field as having a value of a record type. However, this record type
must correspond to the type associated with a concept. The difference between
an object, instance of a concept, and a value of the record-type corresponding
to that concept lies in the identity-integrity mechanism. As said above,
TROEPS
ensures that two objects with the same key cannot be created; this is no longer
true for the record values. Moreover, a concept records the set of its
instances while a type does not record the set of its values. When queried for
the object with a particular key, a concept will return the only object of that
kind if it has been created while a type queried for a value with particular
field values will return a new record with these characteristics regardless to
whether an equal value has been created before or not. Thus, the same query for
the same object returns the same object (identity) while the same query for the
same value returns two different values (equality but not identity). As a
consequence, it is up to the user (or his program) to record the values which
cannot be found by the type system.
This
is generalised to the object/value difference without regarding the fact that
the value is a record, a list or any other kind of value: the object is
identified with its concept and its key while the values are identified by
their structure. This leads to important consequences on keys: an object can
have either another object or a value as the value of a field of its key, but
they are treated differently by
TROEPS:
- If
the object is modified this does not matter since, it is always identifiable by
its key (which cannot be modified).
- The
value cannot be modified (either adding a value to a set, changing a field of a
record or incrementing an integer) because this would be interpreted as
changing it to another value and thus changing the key.
Constructor
The
constructor descriptor indicates whether the value of the field will be a
unique entity (of the type given by the type descriptor), a list of entities
(of the type given by the type descriptor) or a set of entities (of the type
given by the type descriptor). The value of the descriptor is a keyword which
can be
un,
liste
(list) or
ensemble
(set).
A
list is a (possibly empty) ordered collection of entities which can appear more
than once. A set is a (possibly empty) collection of entities with no
repetition. A set is not ordered (thus there is no first nor
nth
element of a set).
Since
these collection constructors are pre-defined in
TROEPS,
TROEPS
provides field accessors for adding elements, removing, testing membership of
entities to these fields. Its is also possible to reach the value as a whole
and to apply classical
TALK
operators on it (see the "object" section).
Nature
Concept
fields are distinguished by their nature. The pre-defined natures for the time
being are
propriete
(property),
composant
(component) and
lien
(link). These are the values admissible for the nature descriptor. The nature
covers quite deep semantic functions of the system and thus some important
reflection have to be carried out before achieving a satisfying extendible
nature system.
The
property is not attached a particular meaning except that the field defines an
object or value which is that of the corresponding property of the object. By
opposition, the component nature is attached to fields with a very precise
semantics.
The
link nature is a mean to define recursive links between objects. The links
introduce restrictions with regard first class properties: they are not taken
into account by classification and filtering algorithms. All the other
functions (e.g. type checking when assigning a link or migrating the object)
are available.
The
study of the composition relation has shown that it contains a plethora of
meanings and could eventually be described as a taxonomy emphasising
functional, homeomerous and separable characteristics. It has shown six
different relations: component/integral object (handle-cup), member/collection
(tree-forest), portion/mass (slice-pie), stuff/object (steel-bike),
feature/activity (paying-shopping) and place/area (oasis-desert). The
composition relation is
functional
when the parts support a functional role with respect to the whole; it is
homeomerous
when the parts are similar to each other and to the whole to which they belong
and it is
separable
when the parts can be separated from the whole to which they are connected. In
TROEPS,
the component/object meaning is used. However, this meaning is so rich that no
checking about it can be made by the system. It is up to the designers of
knowledge bases to take care of this, so that the reasoning they might ask the
system to perform is valid.
The
services provided by
TROEPS
for component fields are the following:
- Existence:
whenever an object with a component field is created (resp. destroyed), the
equivalent value (component) is assumed to exist. This does not prevent,
however, an object of the component type from being created independently.
- Non-cyclicity:
an object cannot be (directly or indirectly) the component of one of its
components.
- Non
sharability: the component of an object cannot be component of another object
except if both objects are also related by (the transitive closure of)
composition fields. This does not prevent it to be referred to as the value of
property or link fields of other objects.
Since
composition is modelled thanks to composite fields, a same object can be
decomposed in many ways, as many as there are viewpoints. For instance, a car
can be composed of the engine, the breaking system, the transmission system,
etc., in a mechanical viewpoint, and can also be composed of its doors, its
body, etc., in a physical viewpoint. On the contrary, one can wish to decompose
an object in the same way in every viewpoint; this can be done by defining
composite fields common to all the viewpoints.
The
transitive reduction of component relations under a viewpoint constitutes a
tree of exclusive branches. The exclusivity of the component nature means that
an object cannot be a component of two different objects unless they are
themselves in a component relation.
Interface

Screendump
8: Concept field display.

Screendump
9: Concept field edition.
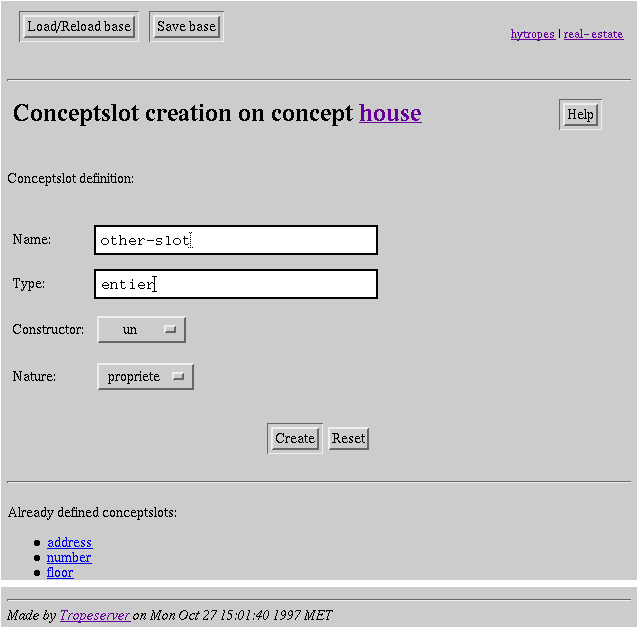
Screendump
10: Concept field creation.
API
- (tr-conceptslot-p
anything) predicate
in [libtrp]
-> boolean,
anything
entity
- Returns
anything
if the argument
anything
is a concept field,
()
otherwise.
- (tr-create-conceptslot
concept
conceptslotname type const nature
) function
in [libtrp]
-> conceptslot,
concept
concept
nak,
conceptslotname
string
nas,adks,
type
string|concept
ivt,
const
string
nas,
ivc
,
nature
string
nas,
ivn
- Creates
and returns a new concept field of name
conceptslotname
in the concept
concept.
It will therefore be known of the system until deletion or initialisation. The
conceptslot is automatically added to the list of fields of the concept
concept
whose
type is updated.
- (tr-find-conceptslot
concept
conceptslotname
) function
in [libtrp]
-> conceptslot,
concept
concept
nak,
conceptslotname
string
nas
- Retrieves
and returns the concept field of name
conceptslotname
in the concept
concept.
When no such concept field is known, returns
().
- (tr-conceptslot
concept
conceptslotname type const nature
) macro
in [libtrp]
-> conceptslot,
concept
concept
nak,
conceptslotname
string
nas,
type
string|concept
ivt,
const
string
nas,
ivc
,
nature
string
nas,
ivn
- Retrieves
and returns the concept field of name
conceptslotname
in the concept
concept.
When no such concept field is known, creates and returns it.
- (tr-delete-conceptslot
conceptslot) function
in [libtrp]
-> boolean,
conceptslot
conceptslot
naks,cmk,
neo
- Deletes
the concept field
conceptslot.
This can only happen if the concept slot is as empty as at its creation and no
classslot with the same name exists in the concept.
- (tr-erase-conceptslot
conceptslot) function
in [libtrp]
-> boolean,
conceptslot
conceptslot
naks,cmk,
neo
- Deletes
the concept field
conceptslot
from the environment. Afterwards neither the conceptslot nor the classslots
refering to it nor the fields of the same name in the objects exist anymore in
the environment.
- (tr-conceptslot-concept
conceptslot) function
in [libtrp]
-> concept,
conceptslot
conceptslot
naks
- Returns
the concept of the concept field
conceptslot.
- (tr-conceptslot-name
conceptslot) function
in [libtrp]
-> string,
conceptslot
conceptslot
naks
- Returns
the name of the concept field
conceptslot.
- (tr-conceptslot-rename
conceptslot
name
) function
in [libtrp]
-> string,
conceptslot
conceptslot
naks,
name
string
nas,
adks
- Changes
the name of the concept field
conceptslot
for the string
name.
This also changes the name of all the corresponding class fields.
- (tr-conceptslot-viewpoints
conceptslot) function
in [libtrp]
-> { conceptview* },
conceptslot
conceptslot
naks
- Returns
the set of concept viewpoints under which the field is visible in its concept.
This set is automatically updated when a class field is declared in a class.
- (tr-get-conceptslot-type
conceptslot) function
in [libtrp]
-> string,
conceptslot
conceptslot
naks
- Returns
the type of the concept field
conceptslot.
- (tr-get-conceptslot-constructor
conceptslot) function
in [libtrp]
-> string,
conceptslot
conceptslot
naks
- Returns
the constructor of the concept field
conceptslot.
- (tr-get-conceptslot-nature
conceptslot) function
in [libtrp]
-> string,
conceptslot
conceptslot
naks
- Returns
the nature of the concept field
conceptslot.
Examples
? (tr-create-conceptslot (tr-find-concept "agent") "segment" "chaine" "un" "propriete")
= (tr-conceptslot (tr-concept "agent") "segment")
? (tr-create-conceptslot (tr-find-concept "agent")
"houses" (tr-find-concept "house") "ensemble" "propriete")
= (tr-conceptslot (tr-concept "agent") "houses")
? (tr-create-conceptslot (tr-find-concept "agent") "subsidiary" "chaine" "un" "propriete")
= (tr-conceptslot (tr-concept "agent") "subsidiary")
? (tr-concept-sorted-slots (tr-find-concept "agent"))
= ((tr-conceptslot (tr-concept "agent") "name")
(tr-conceptslot (tr-concept "agent") "segment")
(tr-conceptslot (tr-concept "agent") "houses")
(tr-conceptslot (tr-concept "agent") "subsidiary"))
? (tr-delete-conceptslot (tr-conceptslot (tr-concept "agent") "subsidiary"))
= t
? (tr-concept-slots (tr-find-concept "agent"))
= ((tr-conceptslot (tr-concept "agent") "houses")
(tr-conceptslot (tr-concept "agent") "name")
(tr-conceptslot (tr-concept "agent") "segment"))
? (tr-create-conceptslot (tr-find-concept "agent") "area" "chaine" "un" "propriete")
= (tr-conceptslot (tr-concept "agent") "area")
? (tr-create-conceptslot (tr-find-concept "agent") "comission" "reel" "un" "propriete")
= (tr-conceptslot (tr-concept "agent") "comission")
? (tr-find-conceptslot (tr-find-concept "agent") "houses")
= (tr-conceptslot (tr-concept "agent") "houses")
? (tr-conceptslot-p (tr-find-conceptslot (tr-find-concept "agent") "name"))
= (tr-conceptslot (tr-concept "agent") "name")
? (tr-conceptslot-p ())
= ()
? (tr-conceptslot-concept (tr-conceptslot (tr-find-concept "agent") "segment"))
= (tr-concept "agent")
? (tr-conceptslot-name (tr-conceptslot (tr-find-concept "agent") "segment"))
= "segment"
? (tr-get-conceptslot-type (tr-conceptslot (tr-find-concept "agent") "segment"))
= "chaine"
? (tr-get-conceptslot-type (tr-conceptslot (tr-find-concept "agent") "houses"))
= (tr-concept "house")
? (tr-get-conceptslot-constructor (tr-conceptslot (tr-find-concept "agent") "segment"))
= "un"
? (tr-get-conceptslot-constructor (tr-conceptslot (tr-find-concept "agent") "houses"))
= "ensemble"
? (tr-get-conceptslot-nature (tr-conceptslot (tr-find-concept "agent") "segment"))
= "propriete"
Viewpoints
Individual
instances of a concept can be seen under different viewpoints -- and thus
described -- from different viewpoints; each viewpoint determines a specific
class hierarchy, and hides some characteristics of a concept (field and class
constraints). In such a way, it is possible to see only the fields concerned
with a viewpoint and to structure the concept in a class hierarchy which is
significant for the viewpoint. The observation of an object through a viewpoint
reveals only a part of its fields. An instance is observable under each
viewpoint, but only a sub-set of its fields. However, the fields of the key are
always visible in each viewpoints in order to be able to identify the objects.
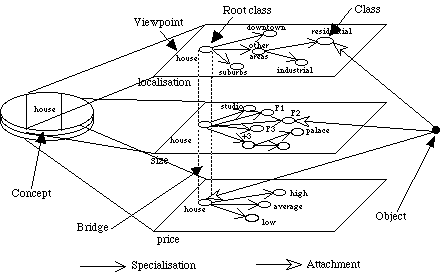
Figure
6: The notions involved in a
TROEPS
knowledge base.
Structure
of a viewpoint
A
viewpoint defines a particular decomposition of the set of objects instance of
the concept. This is materialised by a particular taxonomy of classes proper to
the viewpoint. In a viewpoint, classes are related by the specialisation
relation. A class (so called super-class) is specialised in more restrictive
classes (its sub-classes) which represent sub-sets of the objects attached to
the super-class. The specialisation relation is transitive: a class is a
sub-class of its direct super-class and of its super-classes. Every class is
described inside the viewpoint (see the "class" section).
This
class taxonomy in a viewpoint has a tree structure. The root represents all the
objects of the concept, it has no super-class. The root class is named after
the concept. The root class cannot be constrained (because this could exclude
some instances of the concept). Any other class in the hierarchy has only one
direct super-class.
In
each viewpoint, objects are attached to one and only one class of the class
hierarchy, in which each class represents a set of objects. These viewpoints on
a concept are not totally independent: they communicates through bridges (see
the "bridge" section).
Constraints
on the taxonomy
By
default, in
TROEPS,
taxonomies do not have particular constraints. The classes are descriptions of
(i.e. necessary conditions for belonging to) an intended set of objects but
they are not constrained to be exclusive nor exhaustive. An exclusive taxonomy
is a taxonomy in which the direct sub-classes of a particular class have
pairwise disjoint extensions: an object cannot be member of two of these
classes. An exhaustive taxonomy is one in which the direct sub-classes of a
particular class cover (as a whole) the extension of the super-class: any
object belonging to the super-class is a member of one of its sub-classes.
Lastly, a definitional taxonomy is one for which the extension of the class
exactly corresponds to the set of objects which comply the definition of the
class: the description expresses necessary and sufficient conditions for
belonging to the class.
These defaults can be changed viewpoint by viewpoint. Then
TROEPS
algorithms take advantage of the indications in order to provide more
appropriate results.
Interface
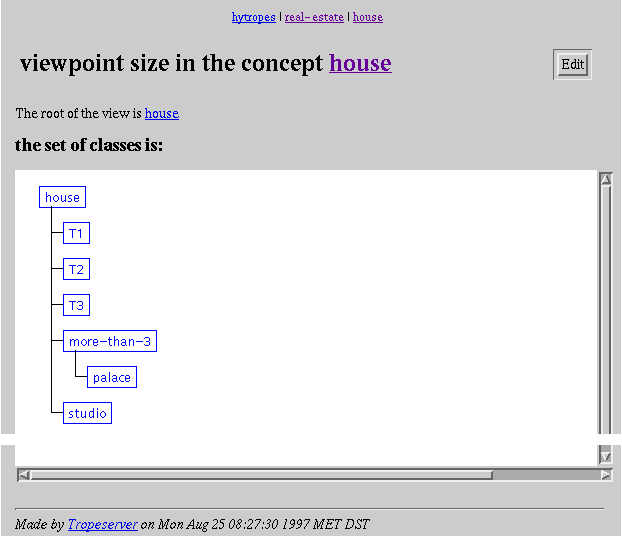
Screendump
11: Viewpoint display.
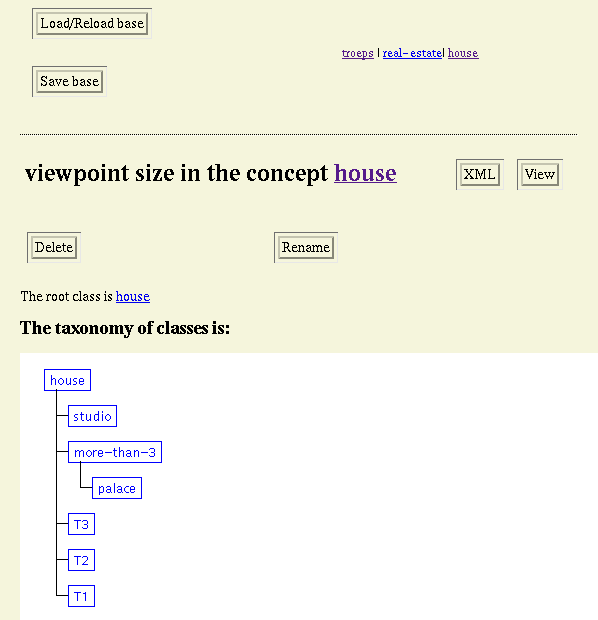
Screendump
12: Viewpoint edition.
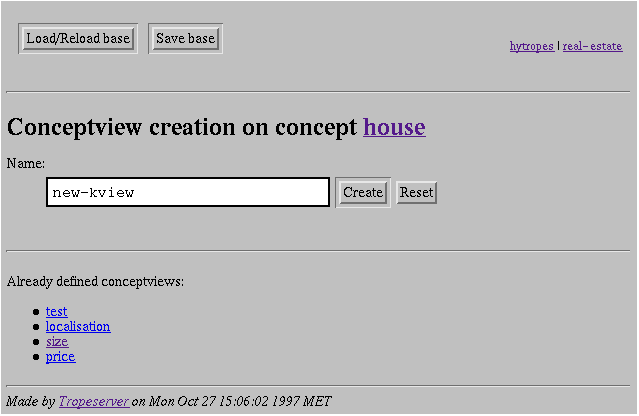
Screendump
13: Viewpoint creation.
API
- (tr-conceptview-p
anything) predicate
in [libtrp]
-> boolean,
anything
entity
- Returns
anything
if the argument
anything
is a concept viewpoint,
()
otherwise.
- (tr-create-conceptview
concept
conceptviewname
) function
in [libtrp]
-> conceptview,
concept
concept
nak,
conceptviewname
string
nas,adkv
- Creates
and returns a new concept viewpoint of name
conceptviewname
in the concept
concept.
It will therefore be known of the system until deletion or initialisation.
- (tr-find-conceptview
concept
conceptviewname
) function
in [libtrp]
-> conceptview,
concept
concept
nak,
conceptviewname
string
nas
- Retrieves
and returns the concept viewpoint of name
conceptviewname
in the concept
concept.
When no such concept viewpoint is known, returns
().
- (tr-conceptview
concept
conceptviewname
) macro
in [libtrp]
-> conceptview,
concept
concept
nak,
conceptviewname
string
nas
- Retrieves
and returns the concept viewpoint of name
conceptviewname
in the concept
concept.
When no such concept viewpoint is known, creates and returns it.
- (tr-delete-conceptview
conceptview) function
in [libtrp]
-> boolean,
conceptview
conceptview
nakv,
neo
- Deletes
the concept viewpoint
conceptview
from
its concept. This can only happen if the concept view is as empty as at its
creation. Afterwards, the concept viewpoint does not exist anymore in the
environment.
- (tr-erase-conceptview
conceptview) function
in [libtrp]
-> boolean,
conceptview
conceptview
nakv,
neo
- Deletes
the concept viewpoint
conceptview
and its content from its concept. Afterwards, neither the concept viewpoint nor
the classes it contains nor the bridges which refer to these classes exist
anymore in the environment.
- (tr-conceptview-concept
conceptview) function
in [libtrp]
-> concept,
conceptview
conceptview
nakv
- Returns
the concept of the concept viewpoint
conceptview.
- (tr-conceptview-name
conceptview) function
in [libtrp]
-> string,
conceptview
conceptview
nakv
- Returns
the name of the concept viewpoint
conceptview.
- (tr-conceptview-rename
conceptview
name
) function
in [libtrp]
-> string,
conceptview
conceptview
nakv,
name
string
nas,
adkv
- Changes
the name of the concept view
conceptview
for the string
name.
- (tr-conceptview-root
conceptview) function
in [libtrp]
-> class,
conceptview
conceptview
nakv
- Returns
the root class of the concept viewpoint
conceptview.
- (tr-conceptview-exhaustive
conceptview
optional:
boolean) function
in [libtrp]
-> boolean,
conceptview
conceptview
nakv,
boolean
boolean
- Sets
(if
boolean
is provided) the exhaustiveness of the concept viewpoint
conceptview
to
boolean
and returns the exhaustiveness of the concept viewpoint.
- (tr-conceptview-exclusive
conceptview
optional:
boolean) function
in [libtrp]
-> boolean,
conceptview
conceptview
nakv,
boolean
boolean
- Sets
(if
boolean
is provided) the exclusiveness of the concept viewpoint
conceptview
to
boolean
and returns the exclusiveness of the concept viewpoint.
- (tr-conceptview-definitional
conceptview
optional:
boolean) function
in [libtrp]
-> boolean,
conceptview
conceptview
nakv,
boolean
boolean
- Sets
(if
boolean
is provided) the definitional character of the concept viewpoint
conceptview
to
boolean
and returns the value of the definitional character of the concept viewpoint.
Examples
? (tr-create-conceptview (tr-concept "agent") "buyer")
= (tr-conceptview (tr-concept "agent") "buyer")
? (tr-create-conceptview (tr-concept "agent") "seller")
= (tr-conceptview (tr-concept "agent") "seller")
? (tr-conceptview-p (tr-find-conceptview (tr-concept "agent") "buyer"))
= (tr-conceptview (tr-concept "agent") "buyer")
? (tr-conceptview-p ())
= ()
? (tr-create-conceptview (tr-concept "agent") "tax-collector")
= (tr-conceptview (tr-concept "agent") "tax-collector")
? (tr-delete-conceptview (tr-conceptview (tr-concept "agent") "tax-collector"))
= t
? (tr-concept-views (tr-find-concept "agent"))
= ((tr-conceptview (tr-concept "agent") "buyer")
(tr-conceptview (tr-concept "agent") "seller"))
? (tr-concept-sorted-views (tr-find-concept "agent"))
= ((tr-conceptview (tr-concept "agent") "buyer")
(tr-conceptview (tr-concept "agent") "seller"))
? (tr-conceptview-concept (tr-conceptview (tr-concept "agent") "buyer"))
= (tr-concept "agent")
? (tr-conceptview-name (tr-conceptview (tr-concept "agent") "buyer"))
= "buyer"
? (tr-conceptview-root (tr-conceptview (tr-concept "agent") "buyer"))
= (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent")
? (tr-conceptview-exhaustive (tr-conceptview (tr-concept "agent") "buyer"))
= ()
? (tr-conceptview-exclusive (tr-conceptview (tr-concept "agent") "buyer"))
= ()
? (tr-conceptview-exclusive (tr-conceptview (tr-concept "agent") "buyer") t)
= t
? (tr-conceptview-exclusive (tr-conceptview (tr-concept "agent") "buyer"))
= t
? (tr-conceptview-definitional (tr-conceptview (tr-concept "agent") "buyer"))
= ()
Class
definition
A
class specifies a virtual set of instances in a concept. This set is described
with the help of restrictions on fields of the objects.
The
class structure
A
class is identified by the viewpoint in which it is defined (which in turns
refers to its concept), a name (unique in a concept viewpoint) and a
super-class. These three elements are mandatory for all classes but the root
classes. Root classes are automatically defined when a viewpoint is defined on
a concept. They have no super-class and their name is that of the concept.
A
class can introduce field restrictions on fields visible under the viewpoint,
this constitutes the set of class fields of a class. The field restrictions are
considered in the next section. A root class, however, cannot introduce any
restriction on the fields because it is meant to represent the whole set of
instances of the concept.
Last,
a class can introduce bridges from it (and other classes in other viewpoints)
to another class (in another viewpoint). Bridges are examined below. A root
class is automatically connected through bridges with the root class of any
other viewpoint of the concept.
Specialisation
The
specialisation relation between classes support several interpretations whose
discussion is out of the scope of this manual. It is expressed by the
transitive closure of the super-class--sub-class link: the sub-class is a
specialisation of the super-class and also specialisation of the classes its
super-class is a specialisation of (see example). A class can have only one
super-class and the root class is the only class which does not have a
super-class. A class can have several sub-classes.
The
specialisation is intended to be exclusive: in the same viewpoint, a particular
instance cannot be a member of two classes which are not in a specialisation
relation. However, the exclusivity is only subjective, this means that the
system cannot warrant it from the definition of the classes. Of course, the
system will signal if one tries to attach an object to two incomparable classes
but it will not be able to decide whether the two classes are really exclusive.
For example, some people once thought that in the person classes, republican
and Quakers were two exclusive classes since republican were reputed to be
bellicists and Quakers pacifists. However, it turned out that Richard Nixon was
both republican and Quaker: he thus must be attached (who said "should have
been"?) to two supposedly exclusive classes.
On
the other hand,
TROEPS
does not suppose that sub-classes are exhaustive (i.e. that any member of a
class must be a member of a sub-class). These two properties are very important
for the determination of the classification algorithms which can take advantage
of the properties. They are also used by other mechanisms (such as the
definition of bridges, see below the "bridge" section).
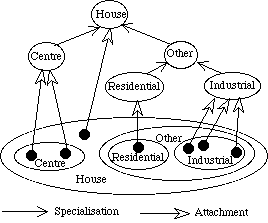
Figure
7: As an example, here, the class-sub-class link is established between
Residential and Other, Industrial and Other, Other and House (the root class).
This means that Residential (and Industrial as well) is a specialisation of
both Other and House. This specialisation is interpreted as the inclusion of
the set of members.
The
specialisation constrains any object attached to a class to be also member of
its super-classes and that any field definition in a class is more (or equally)
restricted than that of its super-classes. Consequently, objects are only
attached to their most specific class and the system is able to infer that they
are member to all of its super classes. Field restrictions do also not have to
be expressed completely. It is sufficient to define only the restrictions from
the super-classes the system will be able to infer the complete type of the
field from the super-classes type restrictions and the new one.
As
an example, in the real estate base, the concept key is
address,
floor
and
number.
Thus, under the
localisation
viewpoint, these three fields are visible. The
center
class is a subclass of the root class (called
house)
of this viewpoint. There are two alternatives for characterising the set of
objects which can be classified under that class:
- Unhiding
a new field called
area
with the possible values in the
center
restricted as {
"grenoble"}.
- Restricting
the addresses to be addresses in the center area (see below for field
restrictions in classes).
Any
house
which is member a of the
center
class will also be a member of the
house
class (of which all houses are members).
Membership
and attachment
An
object is attached to only one class in each viewpoint. It is also said that
the object is member of all super-classes of that class. As a matter of fact,
it is compliant with the field restriction on that class (and thus with the
field restriction of all the super-classes of that class).
So,
while objects are
instances
of a concept, they can only be
attached
to a class. Upon creation, each instance is attached to each root class of each
viewpoint of the concept. The difference is critical for several reasons:
- The
objects can change their attachment class from time to time while they are
always instances of the same concept;
- The
objects can violate the constraints on their classes (they will be
re-classified under the root class) but cannot violate those of the concepts;
- The
concept refers to methods allowing to compute the true value of a field while a
class only refers to methods for guessing a hypothetical value for a field.
The
attachment of an object to a class is a voluntary act from the users (or one of
their programs). This act can be accomplished even if some fields are missing.
The only constraint is that available field values satisfy their types in the
attachment class. However, the consequence of attachment is that unfilled
fields must implicitly satisfy their type as well even if they are unknown.
Interface
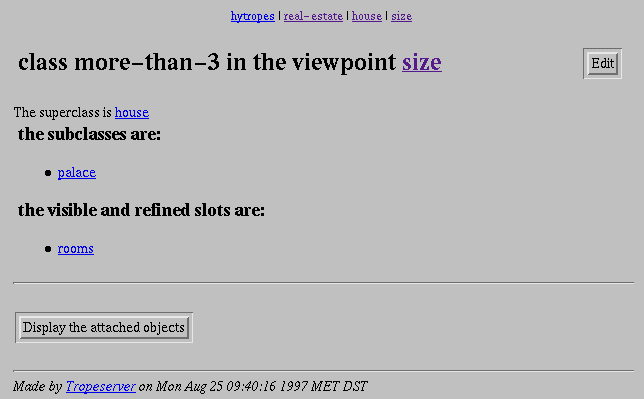
Screendump
14: Class display.

Screendump
15: Class edition.

Screendump
16: Attached objects.
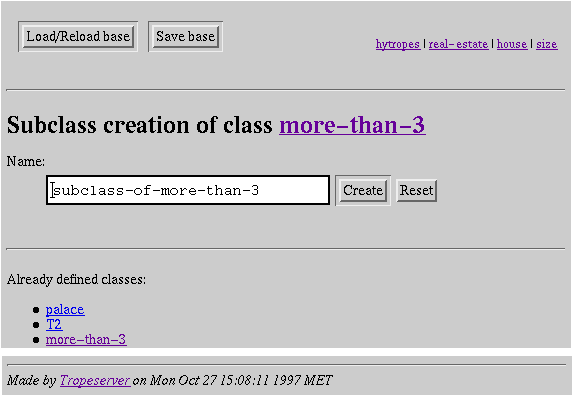
Screendump
17: Class creation.
API
- (tr-class-p
anything) predicate
in [libtrp]
-> boolean,
anything
entity
- Returns
anything
if the argument
anything
is a class,
()
otherwise.
- (tr-create-classsuperclass
classname
) function
in [libtrp]
-> class,,
superclass
class
nac
classname
string
nas,
adc
- Creates
and returns a new class of name
classname.
This class is a specialisation of the class
superclass
and is part of the concept viewpoint of this last class. It will, therefore, be
in the concept viewpoint hierarchy until deletion or initialisation.
- (tr-find-class
conceptview
classnam
e) function
in [libtrp]
-> class,
conceptview
conceptview
nakv,
classname
string
nas
- Retrieves
and returns the class of name
classname
in the concept viewpoint
conceptview.
When no such class is known, returns
().
- (tr-class
conceptview
classname superclass
) macro
in [libtrp]
-> class,
conceptview
conceptview
nakv,
classname
string
nas,
superclass
class
nac,
nikv
- Retrieves
and returns the class of name
classname
in the concept viewpoint
conceptview.
When no such class is known, creates it as a specialisation of the class
superclass
and returns it.
- (tr-delete-class
class) function
in [libtrp]
-> boolean,
class
class
nac,
cdrc, neo
- Deletes
the class
class
from the environment. This leads to its deletion in its concept viewpoint
hierarchy and can only happen if the class is as empty as at its creation.
Afterwards, the class does not exist anymore in the environment.
- (tr-erase-class
class) function
in [libtrp]
-> boolean,
class
class
nac,
cdrc, neo
- Deletes
the class
class
andits content from the environment. Afterwards, neither the class nor its
classslots and constraints nor the bridges which refer to it exist anymore in
the environment.
- (tr-class-conceptview
class) function
in [libtrp]
-> conceptview,
class
class
nac
- Returns
the concept viewpoint of the class
class.
- (tr-class-concept
class) function
in [libtrp]
-> concept,
class
class
nac
- Returns
the concept of the class
class.
- (tr-class-name
class) function
in [libtrp]
-> string,
class
class
nac
- Returns
the name of the class
class.
- (tr-class-rename
class
name
) function
in [libtrp]
-> string,
class
class
nac,
name
string
nas,
adc, crrc
- Changes
the name of the class
class
for the string
name.
The root class name cannot be changed.
- (tr-class-superclass
class) function
in [libtrp]
-> class,
class
class
nac
- Returns
the superclass of the class
class
or
()
if
class
is a root class.
- (tr-class-subclasses
class) function
in [libtrp]
-> { class* },
class
class
nac
- Returns
the set of direct sub-classes of the class
class.
- (tr-class-all-subclasses
class) function
in [libtrp]
-> { class* },
class
class
nac
- Returns
the set of sub-classes of the class
class.
- (tr-class-superclass-p
superclass
class
) function
in [libtrp]
-> boolean,
superclass
classnac,
class
class
nac,
nikv
- Tells
wether the class
superclass
is a superclass (at any level) of the class
class.
- (tr-class-bridges-in
class) function
in [libtrp]
-> { bridge* },
class
class
nac
- Returns
the set of bridges whose destination is the class
class.
- (tr-class-bridges-out
class) function
in [libtrp]
-> { bridge* },
class
class
nac
- Returns
the set of bridges whose source contains the class
class.
- (tr-class-sorted-slots
class
optional: sort-function
) function
in [libtrp]
-> { classslot* },
class
class
nac,
sort-function
function
- Returns
the set of class fields of the class
class
in the creation order of the corresponding conceptslots (or their order in the
base description file) by default. If the
sort-function
is provided, the classslots are sorted according to it.
- (tr-class-slots
class) function
in [libtrp]
-> { classslot* },
class
class
nac
- Returns
the set of class fields of the class
class.
-
(
tr-class-attached
class) function
in [libtrp]
-> { object* },
class
class
nac
- Returns
the set of objects attached to the class
class.
- (tr-class-members
class) function
in [libtrp]
-> { object* },
class
class
nac
- Returns
the set of objects member of the class
class.
Examples
? (tr-create-class
(tr-conceptview-root (tr-conceptview (tr-concept "agent") "buyer")) "good")
= (tr-class (tr-conceptview (tr-concept "agent") "buyer") "good")
? (tr-create-class
(tr-conceptview-root (tr-conceptview (tr-concept "agent") "buyer")) "bad")
= (tr-class (tr-conceptview (tr-concept "agent") "buyer") "bad")
? (tr-create-class
(tr-conceptview-root (tr-conceptview (tr-concept "agent") "seller")) "good")
= (tr-class (tr-conceptview (tr-concept "agent") "seller") "good")
? (tr-create-class
(tr-conceptview-root (tr-conceptview (tr-concept "agent") "seller")) "bad")
= (tr-class (tr-conceptview (tr-concept "agent") "seller") "bad")
? (tr-create-class
(tr-find-class (tr-conceptview (tr-concept "agent") "buyer") "good") "favorite")
= (tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite")
? (tr-create-class
(tr-find-class (tr-conceptview (tr-concept "agent") "buyer") "good") "valuable")
= (tr-class (tr-conceptview (tr-concept "agent") "buyer") "valuable")
? (tr-class-p ())
= ()
? (tr-class-p (tr-find-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
= (tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite")
? (tr-create-class
(tr-find-class (tr-conceptview (tr-concept "agent") "buyer") "good") "not-so-good")
= (tr-class (tr-conceptview (tr-concept "agent") "buyer") "not-so-good")
? (tr-delete-class (tr-class (tr-conceptview (tr-concept "agent") "buyer") "not-so-good"))
= t
? (tr-superclass-p
(tr-find-class (tr-conceptview (tr-concept "agent") "buyer") "good")
(tr-find-class (tr-conceptview (tr-concept "agent") "buyer") "valuable"))
= t
? (tr-superclass-p
(tr-find-class (tr-conceptview (tr-concept "agent") "buyer") "valuable")
(tr-find-class (tr-conceptview (tr-concept "agent") "buyer") "good"))
= ()
? (tr-superclass-p
(tr-find-class (tr-conceptview (tr-concept "agent") "buyer") "valuable")
(tr-find-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
= ()
? (tr-class-conceptview
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
= (tr-conceptview (tr-concept "agent") "buyer")
? (tr-class-concept
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
= (tr-concept "agent")
? (tr-class-name (tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
= "favorite"
? (tr-class-superclass
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
= (tr-class (tr-conceptview (tr-concept "agent") "buyer") "good")
? (tr-class-superclass
(tr-conceptview-root (tr-conceptview (tr-concept "agent") "buyer")))
= ()
? (tr-class-subclasses
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
= ()
? (tr-class-subclasses
(tr-conceptview-root (tr-conceptview (tr-concept "agent") "buyer")))
= ((tr-class (tr-conceptview (tr-concept "agent") "buyer") "bad")
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "good"))
? (tr-class-all-subclasses
(tr-conceptview-root (tr-conceptview (tr-concept "agent") "buyer")))
= ((tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent")
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "bad")
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "good")
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "valuable")
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
? (tr-class-bridges-in
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
= ()
? (tr-class-bridges-out
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
= ()
? (tr-class-slots
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
= ()
? (tr-class-attached
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
= ()
? (tr-class-members
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
= ()
Class
field definition: data typing aspects/unary constraints
Class
fields are used in order to refine the field definition of the members of a
particular class. Some of these fields are devoted to restrict the type of the
values of a field (see the "concept field" section for basic values given in
concepts), some other to indicate that the fields is now visible under the
class. The type refinement is obtained through the addition of field
descriptors which are optional in the definition of a field. They have to be
filled only if this helps restricting the set of acceptable values of the field.
Type
refinement
There
is also a type descriptor in a class field definition. It is used in order to
refine the type descriptor used in the concept. As in the concept case, it must
be distinguished between types and classes.
For
types, the type descriptor can only contain a sub-type of the initial type: for
instance, it can be the ASCII-string as a sub-type of string. The reader should
report to the "type" section (Appendix
5)
in order to fully understand and use types and sub-types. Record types have
implicit subtypes which are expressed exactly as subclasses types (this is
translated by the system).
For
classes, the field is refined by specifying a set of classes (of the same
concept but different viewpoints) the value (an object here) must be member of.
The meaning of that set of classes is that the object to fill the field must be
a member of each class in the set. Of course, these classes are classes of the
concept and the set of classes can only contain classes which are subclasses of
classes in the super-class type specification (by default, if there is no
restriction, it is intended that the root class of each missing viewpoint is in
the set).
Advanced
type refinement
Advanced
type refinement applies to fields whose values are objects. It allows to add
constraints on the possible values of the fields. This is achieved by defining
a sub-class of a particular class which is called filter (see above the "class"
section) and to add more field constraints on that class. A filter is defined
exactly as a class (with a super-class, a viewpoint and a name), it usually
contains more field restrictions and even more inference methods than the
initial class but:
- It
does not appear in the specialisation graph of its viewpoint;
- No
object is properly attached to a filter.
It
defines the set of admissible values as the objects which are member of its
super-classes and which satisfy the restrictions of the filter. Such a filter
is different from a filter used as an inference method in the use which is made
of it.
An
example of filter is the houses located in the center with more than 3 rooms.
Enumeration
The
domain descriptor enumerates the set of possible values that can be in the
field value. As an example, the
center
class will restrict the
area
field value (whose type is
chaine,
i.e. string) to be
"grenoble".
In case of collection types, it is possible to specify a set of sets or a set
of lists as a domain.
Exclusion
The
except descriptor enumerates a set of values which cannot be the value of the
field. For instance, the set of
address
in the
residential
class will exclude values among
"factory
St."
and
"big
garbage dr."
.
In case of collection types, it is possible to exclude a set of sets or a set
of lists from the possible values.
Unary
constraints
The
condition descriptor contains a list of unary predicates which must be
satisfied by the values of the fields. For the definitions of unary constraints
or predicates, see next chapter. There is no pre-defined constraints in
TROEPS.
These predicates are checked against the whole value of the field. The value of
the field must thus satisfy all the given predicates. For example, if the
numbers in a street are (as in some European towns) odd on one side and even on
the other, it is possible to delimit the district only by the numbers which are
odd in a street (it is sometime usual to have one side in a district and the
other side on the other, guess what? the "bec-de-gaz" are different from side
to side).
Intervals
The
intervals descriptor applies to ordered types. Types such as integer, real and
strings are ordered. It is also possible to define order on other types and to
define ordered concepts. The value of such a descriptor is a list of
TROEPS
interval structures. This restriction means that the field value must belong to
one of the given intervals. As an example, under the
price
viewpoint, the
average
class constrains the
rent
field to be in the interval
{[10000.
15000.]}
.
As
an example, these intervals are obtained by the following
TALK
instructions:
[45 52] => (tr-make-interval 45 t 52 t)
[45 52[ => (tr-make-interval 45 t 52 ())
]45 52] => (tr-make-interval 45 () 52 t)
]45 52[ => (tr-make-interval 45 () 52 ())
]-[infinity] +[infinity][ => (tr-make-interval '-inf () '+inf ())
Cardinality
The
cardinal descriptor only applies to collection types. It allows to restrict the
cardinal (for a set and length for a list) to be a particular positive integer
or within a positive integer interval (including +[infinity]). It can be
expressed with a positive integer interval. For instance, under the
size
viewpoint, the
more-than-3
rooms class constrains the cardinal of the
rooms
field to be superior to 3 (i.e. in
]3
+inf[
).
Interface

Screendump
18: Class field display.
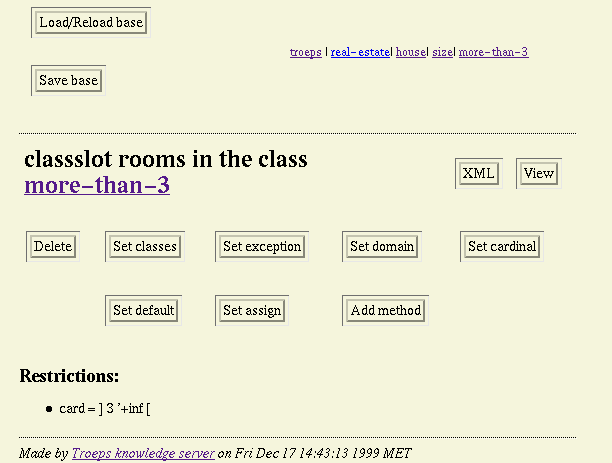
Screendump
19: Class field edition.
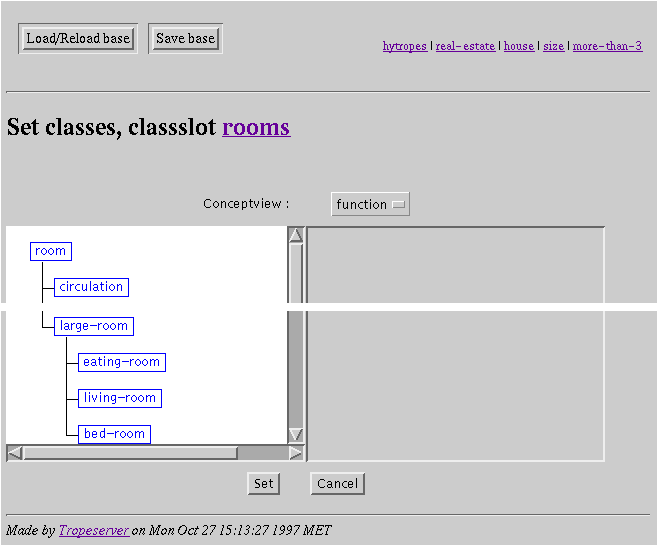
Screendump
20: Class field typing modification.
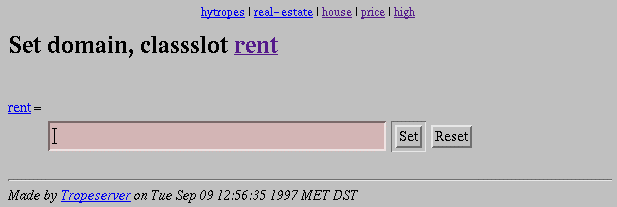
Screendump
21: Class field domain modification.
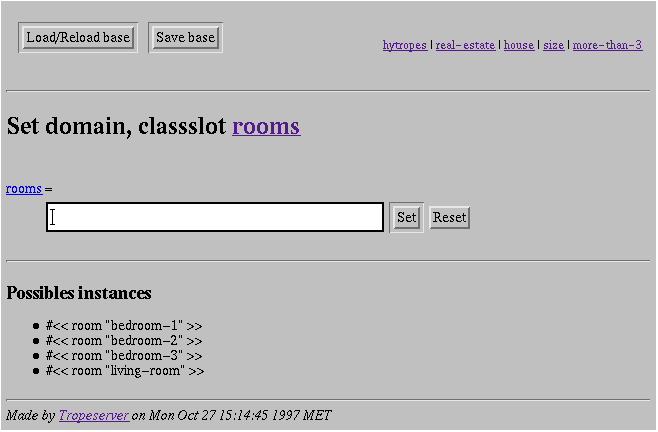
Screendump
22: Class field except modification.
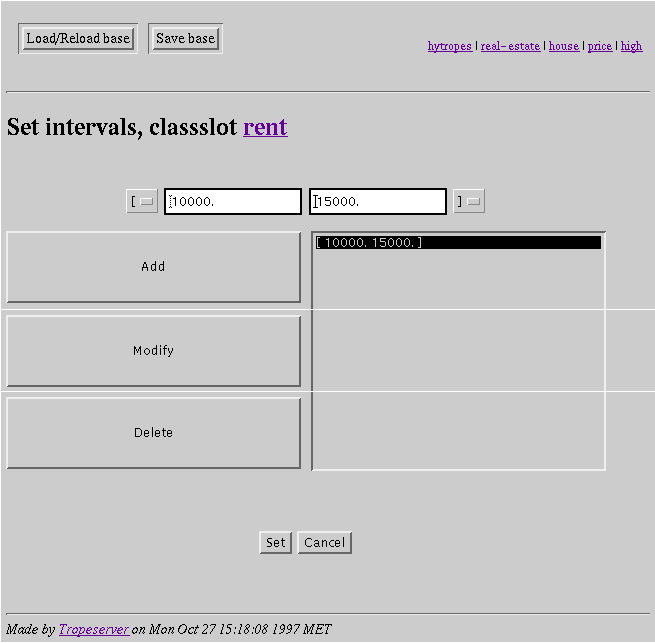
Screendump
23: Class field intervals modification.
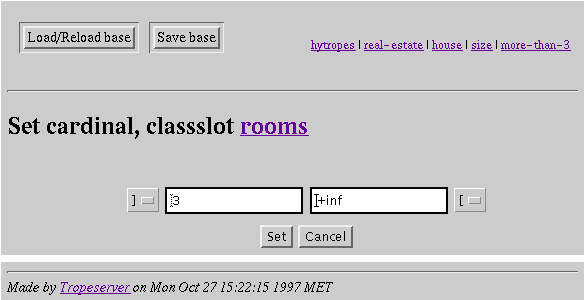
Screendump
24: Class field cardinality modification.
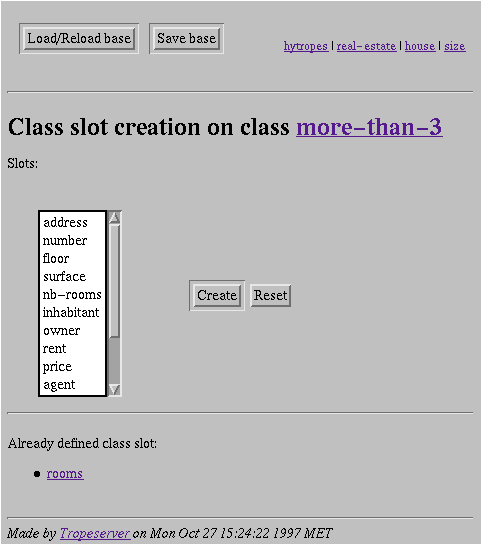
Screendump
25: Class field creation.
API
- (tr-classslot-p
anything) predicate
in [libtrp]
-> boolean,
anything
entity
- Returns
anything
if
the argument
anything
is a class field,
()
otherwise.
- (tr-create-classslot
class
classslotname
) function
in [libtrp]
-> classslot,
class
class
nac,
classslotname
string
nas,
niks, adcs
- Creates
and returns a new class field of name
classslotname
in the class
class.
The corresponding concept field is then visible under the concept viewpoint of
the class. It will therefore be known of the system until deletion or
initialisation.
- (tr-find-classslot
class
classslotname
)
function
in [libtrp]
->classslot,
class
class
nac,
classslotname
string
nas,
niks
- Retrieves
and returns the class field of name
classslotname
in the class
class.
When no such class field is known, returns
().
- (tr-classslot
class
classslotname
) macro
in [libtrp]
-> classslot,
class
class
nac,
classslotname
string
nas,
niks
- Retrieves
and returns the class field of name
classslotname
in the class
class.
When no such class field is known, creates and returns it.
- (tr-delete-classslot
classslot) function
in [libtrp]
-> boolean,
classslot
classslot
nacs,
neo
- Deletes
the class field
classslot
from the environment. If there is no class field corresponding to the same
concept field as
classslot
in the viewpoint, then the concept field is not visible anymore under the
concept viewpoint. Afterwards, the class field does not exist anymore in the
environment.
- (tr-erase-classslot
classslot) function
in [libtrp]
-> boolean,
classslot
classslot
nacs,
neo
- Deletes
the class field
classslot
from the environment. Afterwards, the class field does not exist anymore in the
environment.
- (tr-classslot-name
classslot) function
in [libtrp]
-> string,
classslot
classslot
nacs
- Returns
the name of the class field
classslot.
- (tr-classslot-class
classslot) function
in [libtrp]
-> class,
classslot
classslot
nacs
- Returns
the class of the class field
classslot.
- (tr-classslot-conceptslot
classslot) function
in [libtrp]
-> conceptslot,
classslot
classslot
nacs
- Returns
the concept field corresponding to the class field
classslot.
- (tr-get-classslot-type
classslot) function
in [libtrp]
-> { class* },
classslot
classslot
nacs
- Returns
the type of the class field
classslot,
()
if it is not refined in the class field.
- (tr-set-classslot-type
classslot
type
) function
in [libtrp]
-> boolean,
classslot
classslot
nacs,
type
{ class
ivt*
}
ivt,
adf
- Refines
the type of the class field
classslot
by setting it to the new type
type.
- (tr-get-classslot-domain
classslot) function
in [libtrp]
-> { entity* },
classslot
classslot
nacs
- Returns
the domain of the class field
classslot,
()
if it is not refined in the class field.
- (tr-set-classslot-domain
classslot
domain) function
in [libtrp]
-> boolean,
classslot
classslot
nacs,
domain
{ entity* }
ivd,
adf
- Refines
the domain of the class field
classslot
by restricting it to the new domain
domain.
- (tr-get-classslot-except
classslot)
function
in [libtrp]
-> { entity* },
classslot
classslot
nacs
- Returns
the exceptions of the class field
classslot,
()
if they are not refined in the class field.
- (tr-set-classslot-except
classslot
domain) function
in [libtrp]
-> boolean,
classslot
classslot
nacs,
domain
{ entity* }
ive,
adf
- Refines
the exceptions of the class field
classslot
by retracting the new domain
domain.
- (tr-get-classslot-intervals
classslot)
function
in [libtrp]
-> { interval* },
classslot
classslot
nacs
- Returns
the intervals of the class field
classslot,
()
if they are not refined in the class field.
- (tr-set-classslot-intervals
classslot
intervals) function
in [libtrp]
->
boolean,
classslot
classslot
nacs,
intervals
( interval* )
ivi,
adf
- Refines
the intervals of the class field
classslot
by restricting them to the new intervals
intervals.
- (tr-get-classslot-card
classslot)
function
in [libtrp]
-> interval,
classslot
classslot
nacs
- Returns
the cardinal of the class field
classslot,
()
if it is not refined in the class field.
- (tr-set-classslot-card
classslot
interval
) function
in [libtrp]
-> boolean,
classslot
classslot
nacs,nct,
interval
intervalivcd,
adf
- Refines
the cardinal interval of the class field
classslot
by restricting it to the new interval
interval.
Examples
? (tr-classslot-p
(tr-create-classslot
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent") "comission"))
= (tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent") "comission")
? (tr-find-classslot
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent") "comission")
= (tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent") "comission")
? (tr-create-classslot
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent")
"houses")
= (tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent") "houses")
? (tr-classslot-name
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent")
"comission"))
= "comission"
? (tr-classslot-class
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent")
"comission"))
= (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent")
? (tr-get-classslot-intervals
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent")
"comission"))
= #s(<undef>)
? (tr-set-classslot-intervals
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent")
"comission")
(list (tr-make-interval 0. t 100. t)))
= ((tr-make-interval 0. t 100. t))
? (tr-get-classslot-intervals
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent")
"comission"))
= ((tr-make-interval 0. t 100. t))
? (tr-set-classslot-intervals
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "good")
"comission")
(list (tr-make-interval 0. t 7. t)))
= ((tr-make-interval 0. t 7. t))
? (tr-set-classslot-intervals
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "bad")
"comission")
(list (tr-make-interval 7. () 100. t)))
= ((tr-make-interval 7. () 100. t))
? (tr-set-classslot-domain
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent")
"area")
(list "meylan" "grenoble" "echirolles" "crolles" "montbonnot"
"eybens" "saint-martin d'heres" "fontaine" "sassenage"
"sessinnet" "saint-egreve"))
= ("meylan" "grenoble" "echirolles" "crolles" "montbonnot" "eybens"
"saint-martin d'heres" "fontaine" "sassenage" "sessinnet" "saint-egreve")
? (tr-set-classslot-except
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "valuable")
"area")
(list "meylan" "grenoble" "crolles" "montbonnot"
"saint-martin d'heres"))
= ("meylan" "grenoble" "crolles" "montbonnot" "saint-martin d'heres")
? (tr-get-classslot-except
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "valuable")
"area"))
= ("meylan" "grenoble" "crolles" "montbonnot" "saint-martin d'heres")
? (tr-set-classslot-domain
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite")
"area")
(list "meylan" "grenoble" "crolles" "montbonnot"
"saint-martin d'heres"))
= ("meylan" "grenoble" "crolles" "montbonnot" "saint-martin d'heres")
? (tr-get-classslot-domain
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite")
"area"))
= ("meylan" "grenoble" "crolles" "montbonnot" "saint-martin d'heres")
? (tr-set-classslot-type
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite")
"houses")
(list
(tr-find-class (tr-find-conceptview (tr-find-concept "house") "size") "palace")))
= ((tr-class (tr-conceptview (tr-concept "house") "size") "palace"))
? (tr-get-classslot-type
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite")
"houses"))
= ((tr-class (tr-conceptview (tr-concept "house") "size") "palace"))
? (tr-set-classslot-card
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite")
"houses")
(tr-make-interval 30 t '+inf ()))
= (tr-make-interval 30 t '+inf ())
? (tr-get-classslot-card
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite")
"houses"))
= (tr-make-interval 30 t '+inf ())
? (tr-delete-classslot
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent")
"houses"))
= t
? (tr-class-slots
(tr-find-class (tr-find-conceptview (tr-find-concept "agent") "buyer") "agent"))
= ((tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent") "area")
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent") "comission")
? (tr-class-sorted-slots
(tr-find-class
(tr-find-conceptview
(tr-find-concept "agent")
"buyer")
"agent"))
= ((tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent") "area")
(tr-classslot (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent") "comission")
Filters
The
structure of filters is the same as those of classes but they are not
considered as classes. A filter is a definitional class description attached to
a concept or to a set of classes (from different viewpoints). It aims at
collecting the set of instances which satisfy its constraints. The filter is
satisfied by any instance (of the concept or member of the above classes) which
satisfies the constraints defined by the filter. They can be used for various
tasks (related to instance retrieval). In particular, filters are used for
specifying authorised field values (see the "Class field definition: data
typing aspects/unary constraint" section) and inferring possible field values
(see the "Computation by filter" section in the "Computing field values" part).
A
filter is created through a special function and can be manipulated exactly as
a class by adding constraints on it and retrieving its members through
tr-class-member).
However, filters do not have sub-classes (or sub-filters).
Note
that filters are the only element which are not recoverable from their printed
forms (i.e. cut and paste of a filter from the result of its creation will not
return the filter).
Interface
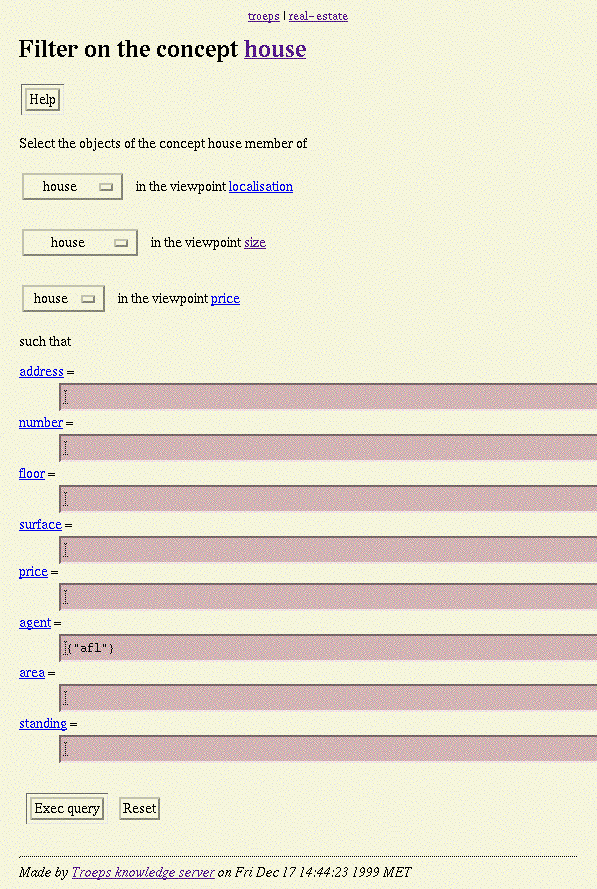
Screendump
26: Filter creation, edition and execution.

Screendump
27: Filter result.
API
- (tr-filter-p
anything) function
in [libtrp]
->
boolean,
anything
entity
- Creates
and returns a new filter from class
class
with no more constraint than the class
class.
- (tr-create-filter
concept rest:
classes) function
in [libtrp]
->
filter,
concept
concept
nak,
classes
{ class
nac*
}
ivb
- Creates
and returns a new filter in concept concept from classes
classes
with no more constraint than those of the classes.
- (tr-delete-filter
filter) function
in [libtrp]
->
boolean,
filter
filternaft,
neo
- Deletes
the filter
filter.
This inhibits it. This can only happen if the filter is as empty as at its
creation: i.e. it has no classslots nor constraints. Afterwards, the filter
does not exist anymore in the environment.
- (tr-erase-filter
filter) function
in [libtrp]
->
boolean,
filter
filternaft,
neo
- Deletes
the filter
filter
and its classslots and constraints.
- (tr-filtered-objects
filter) function
in [libtrp]
->
( object* ),
filter
filternaft
- Returns
the set of objects which satisfy the filter
filter.
- (tr-concept-proper-filters
concept) function
in [libtrp]
->
( filter* ),
concept
conceptnak
- Returns
the set of filters of the concept
concept
which are not attached to any class.
- (tr-class-proper-filters
class) function
in [libtrp]
->
( filter* ),
class
classnac
- Returns
the set of filters directly attached to the class
class.
- (tr-class-filters
class) function
in [libtrp]
->
( filter* ),
class
classnac
- Returns
the set of filters indirectly attached under the class
class.
Examples
? (tr-class-proper-filters
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "good"))
= ()
? (setf my-filter
(tr-create-filter
(tr-concept "agent")
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "good")))
= (tr-filter (tr-concept "agent"))
? (tr-class-proper-filters
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "good"))
= ((tr-filter (tr-concept "agent")))
? (tr-class-proper-filters
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent"))
= ()
? (tr-class-filters
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent"))
= ((tr-filter (tr-concept "agent")))
? (tr-filter-p my-filter)
= (tr-filter (tr-concept "agent"))
? (tr-concept-proper-filter (tr-concept "agent"))
= ()
? (tr-class-filters
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent"))
= ((tr-filter (tr-concept "agent")))
? (tr-filtered-objects my-filter)
= ()
? (setf my-other-filter (tr-create-filter (tr-concept "agent")))
= (tr-filter (tr-concept "agent"))
? (eq my-filter my-other-filter)
= ()
? (tr-concept-proper-filters (tr-concept "agent"))
= ((tr-filter (tr-concept "agent")))
Bridges
Viewpoints
define class hierarchies which are not completely independent. As an example,
in the
house
concept it is known that the objects which are members of the
residential
area under the
localisation
viewpoint and the
more-than-3
room class under the
size
viewpoint are also in the class of
high
priced houses under the
price
viewpoint. This is expressed with the help of bridges.
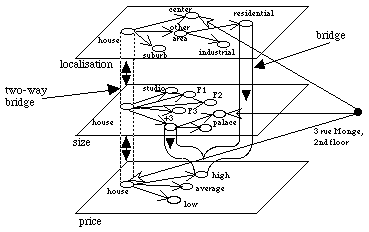
Figure
8: The
house
concept augmented with a bridge asserting that the houses located in a
residential
area with more than
three
rooms must have a
high
price. Other (bi-directional) bridges are those related the root classes of the
viewpoints.
A
bridge has a name and is made of a source which is a set of classes and a
destination which is a class in another viewpoint. Thus, unlike a real bridge, a
TROEPS
bridge is oriented. It asserts that each member of all the source classes is
also a member of the destination class.
This
entails some consequences among which:
- The
(combination of the) field restrictions of the sources classes can be inferred
as having more (or the same) restrictions than the destination class.
Installing bridges between classes does not lead to any consequence on the
visibility of fields. However, it has consequences on how the field values
(even hidden) are constrained. For instance, if any residential house must be
high priced, this means that a particular house is not subject to be classified
in the residential class when it is low priced, and this, even if the price
field is not visible under the localisation viewpoint (see the "classification"
section for more details about this).
- The
source classes must all be from different viewpoints (otherwise, the bridge is
either redundant or contradictory). The destination class must be from a
different viewpoint than the viewpoints of source classes (otherwise this would
result either in asserting that some classes are empty or some other -- related
by specialisation -- are the same by definition).
Note
that, conceptually, the root class of each viewpoint is related by a bridge
with any other root class of any other viewpoint (represented as bi-directional
bridges on the picture). However, these implicit bridges are not physically
represented in
TROEPS.
So, it is not possible to find them through the bridge related functions of
concepts and classes.
Further
constraints must be satisfied when installing bridges: a bridge must not lead
to a contradiction in the inclusion relations induced by specialisation. As a
matter of fact, some points are deduced by
TROEPS:
- Each
pair of bridges with the same source can only have, as destinations, classes
related by specialisation.
- When
considering a first viewpoint with a class
A
and two subclasses
A'
and
A",
a second viewpoint with a class
B
and two sub-classes
B'
and
B"
plus two one-way bridges from
B'
to
A
and from
A'
to
B,
it can be deduced that (1)
A"
and
B"
are empty (2)
A,
A',
B,
B'are
the same class.
- Concerning
circularity detection among bridges, the system detects and refuses only one
kind of circular bridge sets: those which constrain any object triggering the
bridge to migrate in a class non comparable with one of the sources of the
bridge (see
Figure
9
).
Figure
9: Examples of a circularity prohibited by
TROEPS
(a) and two others (b and c) non prohibited.
Finally,
TROEPS
is able to detect subsumption among bridges and to warn the user of this. The
semantics of bridge subsumption is that a bridge is subsumed by another if and
only if any possible object falling under it would also fall under the other
and their destination classes are in specialisation relation. More formally, a
bridge is subsumed by another if and only if for each class in the source of
the latter there exists a super-class of it in that of the former and the
destination of the former is a super-class of that of the latter. As an example,
Figure
10
illustrates the fact that B1 is subsumed by B2 and B3 but B2 and B3 are non
comparable by bridge subsumption since if all objects which fall under B3 also
fall under B2, B3 is more precise than B2 (it leads to a more specific class).
Figure
10: Bridge subsumption example: B1 is subsumed by both B2 and B3.
Interface
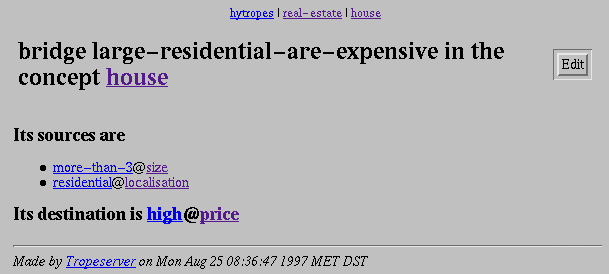
Screendump
28: Bridge display.

Screendump
29: Bridge edition.

Screendump
30: Bridge creation and modification.
API
-
(
tr-bridge-p
anything) predicate
in [libtrp]
-> boolean,
anything
entity
- Returns
anything
if the argument
anything
is a bridge,
()
otherwise.
- (tr-create-bridge
concept name source destination
) function
in [libtrp]
-> bridge,
concept
concept
nak,
name
string
nas,adb,,
source
{ class
nac*
}
ivbp
,
destination
class
nac
- Creates
and returns a new bridge between the source classes
source
and the destination class
destination.
This bridge is automatically inserted in the list of bridges of the concept and
the lists of bridges of the concerned classes. The consequences of the bridge
establishment on the types of classes under the different viewpoints are
computed and notified.
Error
messages: bik, rbb, rba
- (tr-find-bridge
concept
bridgename
)
function
in [libtrp]
->bridge,
concept
concept
nak,
bridgename
string
nas
- Retrieves
and returns the bridge of name
bridgename
in the concept
concept.
When no such bridge is known, returns
().
- (tr-bridge
concept
bridgename source destination
)
function
in [libtrp]
->bridge,
concept
concept
nak,
bridgename
string
nas,
source
{ class
nac*
}
ivbp
,
destination
class
nac
- Retrieves
and returns the bridge of name
bridgename
in the concept
concept.
When no such bridge is known, creates and returns it.
- (tr-delete-bridge
bridge
) function
in [libtrp]
-> boolean,
bridge
bridge
nap,
neo
- Deletes
the bridge
bridge
from its concept. The bridge is automatically removed from the list of bridges
of the concept and the list of bridges of source and destination classes.
- (tr-erase-bridge
bridge
) function
in [libtrp]
-> boolean,
bridge
bridge
nap,
neo
- Deletes
the bridge
bridge
from its concept. The bridge is automatically removed from the list of bridges
of the concept and the lists of bridges of source and destination classes.
- (tr-bridge-concept
bridge
) function
in [libtrp]
-> concept,
bridge
bridge
nap
- Returns
the concept of the bridge
bridge.
- (tr-bridge-name
bridge
) function
in [libtrp]
-> string,
bridge
bridge
nap
- Returns
the name of the bridge
bridge.
- (tr-bridge-rename
bridge
name
) function
in [libtrp]
-> string,
bridge
bridge
nap,
name
string
nas,
adp
- Changes
the name of the bridge
bridge
for the string
name.
- (tr-bridge-source
bridge
) function
in [libtrp]
-> { class* },
bridge
bridge
nap
- Returns
the set of source classes of the bridge
bridge.
- (tr-bridge-destination
bridge
) function
in [libtrp]
-> class,
bridge
bridge
nap
- Returns
the destination class of the bridge
bridge.
Examples
? (tr-bridge-p ())
= ()
? (tr-bridge-p
(tr-create-bridge
(tr-concept "agent") "bad-agents-are-preferable"
(list (tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
(tr-class (tr-conceptview (tr-concept "agent") "seller") "bad")))
= (tr-bridge (tr-concept "agent") "bad-agents-are-preferable")
? (tr-class-bridges-in (tr-class (tr-conceptview (tr-concept "agent") "seller") "bad"))
= ((tr-bridge (tr-concept "agent") "bad-agents-are-preferable"))
? (tr-class-bridges-out
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
= ((tr-bridge (tr-concept "agent") "bad-agents-are-preferable"))
? (tr-concept-bridges (tr-concept "agent"))
= ((tr-bridge (tr-concept "agent") "bad-agents-are-preferable"))
? (tr-bridge-concept (tr-bridge (tr-concept "agent") "bad-agents-are-preferable"))
= (tr-concept "agent")
? (tr-bridge-name (tr-bridge (tr-concept "agent") "bad-agents-are-preferable"))
= "bad-agents-are-preferable"
? (tr-bridge-source (tr-bridge (tr-concept "agent") "bad-agents-are-preferable"))
= ((tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite"))
? (tr-bridge-destination (tr-bridge (tr-concept "agent") "bad-agents-are-preferable"))
= (tr-class (tr-conceptview (tr-concept "agent") "seller") "bad")
Objects
An
object is an instance of a concept. It is made of a collection of field values
corresponding to fields defined in the concept. Fields, but key fields, can be
unfilled (i.e. have no value). For a value of the key there exists only one
corresponding object. This ensure the identity and the identifiability of the
object. An object may evolve during its life-cycle (from its creation to its
deletion) but the key field values cannot change.
As
an example, in the real estate base, a particular house is represented by an
instance of the house concept whose
address
is
"rue
Monge"
,
number
is
3,
floor
is
2,
area
is
"Latin
quarter"
(I know you knew),
rent-price
is
4500.
(Yeah, these are French francs) and
nb-rooms
is
2
(so, you cannot come with your kids). It is noteworthy that
TROEPS
is suited to real estate purpose since it is possible to have unfilled fields
such as the one concerning the
surface
(floor dimension) of the apartment. Since the key of a house instance is the
address
plus a
floor
plus a
number,
this house is uniquely identified and that is why the mail can reach it
(however, for mail concerning
TROEPS,
you can send it to the address in the introductory note, thanks).
An
instance is attached to one and only one class, for each viewpoint. This is
described by the
is-in
field, the value of which is the set of classes of the object (when there is no
class for a viewpoint, it is assumed that the value is the root class of that
viewpoint). This object is attached to the
average
(for Paris of course) class under the
price
viewpoint, the
center
for the
localisation
viewpoint and the
F2
for the
size
viewpoint. The instance belongs to its initial class and to any of its
super-classes, under each viewpoint. Of course, all the field values of the
above instance (the one whose
address
is
"rue
Monge"
,
number
is
3
and whose
floor
is
2)
satisfy the constraints put on them by the different classes. Moreover, even
the unknown fields must satisfy the constraints (so, it is considered that the
real value of the field satisfies them). This is asserted by the fact that the
user (or one of his programs) has (voluntarily) attached the object to the
class. For instance, the real estate agent lets the customer think that there
is a bridge from a flat whose
rent-price
is higher than
4000
Francs
and a flat whose
surface
is more than
40
m
2.
Such a bridge would enable to deduce that the
size
of the above flat is more than
40
m
2.
However, there is no such bridge in the base (read your contract again).
A
complete instance, when considered from a global viewpoint, shows its complete
information, i.e. values for each field of the concept. On the other hand, when
considered under a specific viewpoint, only fields known under this viewpoint
can be seen, so a viewpoint provides a partial view on the instance (any other
field is hidden under the viewpoint). As an example, the object representing
the house described above has an
address,
door
number,
floor
number under each viewpoint plus:
- a
number of
room
under the
size
viewpoint;
- a
rent-price
under the
price
viewpoint (yeah, the extra charge is also unfilled);
- an
area
under the
localisation
viewpoint.
Class
definition, attachment and values
There
is a subtle game between class definition, attachment and field values. As a
matter of fact, any change of one of them must comply with the definition of
the others: changing attachment can only be done if the slot values comply with
the new class definition, changing a slot value can only be achieved if the
value complies with the definition of the current attachment classes and
changing a class definition requires that the attached objects complies the new
definition.
In
the current implementation, such an operation can only be achieved if it does
not conflict with the others. This also applies to the knowledge bases in
textual format.
Interface
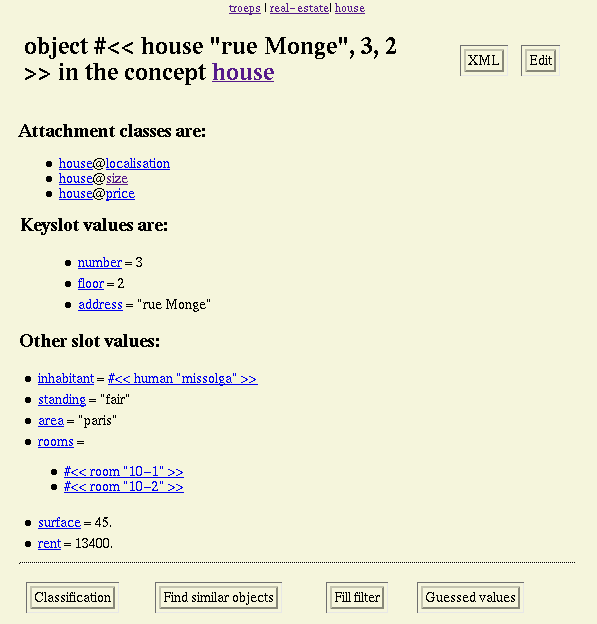
Screendump
31: Object display.
Screendump
32: Object edition. The key field values are not editable.
Screendump
33: Object creation and modification.
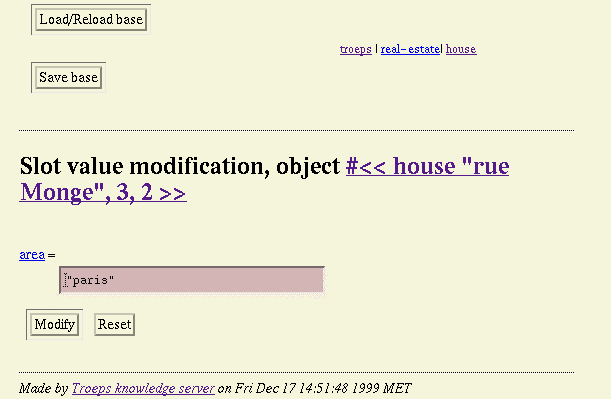
Screendump
34: Field value modification.

Screendump
35: Object attachment.
API
- (tr-object-p
anything) predicate
in [libtrp]
-> boolean,
anything
entity
- Returns
anything
if the argument
anything
is an object,
()
otherwise.
- (tr-create-object
concept keyval
) function
in [libtrp]
->
object,
concept
concept
nak,
keyval
( entity* )
ivk,
aeo
- Creates
and returns a new instance of the concept
concept
with the key specified by the list of key field values
keyval.
It will therefore be known of the system until deletion or initialisation.
- (tr-create-complete-object
concept classlist slotvallist
) function
in [libtrp]
->
object,
concept
concept
nak,
classlist
{ class
nac*
}
ivps,
slotvallist
{ (string
nas,nsa
. entity)
btv*
}
ivk,
aeo
- Creates
and returns a new instance of the concept
concept
with the list of field values given in
slotvallist
(which must at least contain the values for key slots). The created object is
attached to the classes in
classlist.
It will be known of the system until deletion or initialisation.
- (tr-find-object
concept
keyval
) function
in [libtrp]
->
object,
concept
concept
nak,
keyval
( entity* )
ivk
- Retrieves
and returns the instance of concept
concept
with key
keyval.
When no such object is known, returns
().
- (tr-object
concept
keyval
) macro
in [libtrp]
-> object,
concept
concept
nak,
keyval
( entity* )
ivk
- Retrieves
and returns the instance of concept
concept
with key
keyval.
When no such object is known, creates and returns it.
- (tr-delete-object
object
) function
in [libtrp]
-> boolean,
object
object
nao,
neo
- Deletes
the object
object
from the environment. Afterwards, the object does not exist anymore in the
environment.
- (tr-erase-object
object
) function
in [libtrp]
-> boolean,
object
object
nao,
neo
- Deletes
the object
object
from the environment. Afterwards, the object does not exist anymore in the
environment.
- (tr-object-key
object
) function
in [libtrp]
-> ( entity* ),
object
object
nao
- Returns
the list of key field values of the object
object.
- (tr-object-concept
object
) function
in [libtrp]
(tr-is-a
object
) macro
in [libtrp]
-> concept,
object
object
nao
- Returns
the concept of the object
object.
- (tr-is-in
object rest: views
) function
in [libtrp]
-> { class* },
object
object
nao,
views
{ conceptview
nakv*
}
ivsp
- Returns
the set of classes to which the object
object
is attached. If the optional set of concept views
views
is provided, only the classes in the concerned views are returned.
- (tr-is-in-under
object conceptview
) function
in [libtrp]
-> class,
object
object
nao,
conceptview
conceptview
nakv
- Returns
the class to which the object
object
is attached under the concept viewpoint
conceptview.
- (tr-attach
object class
) function
in [libtrp]
-> class,
object
object
nao,
class
class
nac,
nik
- Attaches
the object
object
to the class
class.
The previous attachment class of the object under the same concept viewpoint is
no longer valid. Note that the compliance of the object with the class
definition is checked before attachment; in case of failure, nothing is changed.
- (tr-set-value
object slotname value rest: views
) function
in [libtrp]
-> boolean,
object
object
nao,
slotname
string
nas,
ukks
,value
entity
ivsv,
cmk, kcv, ccv
,
views
{ conceptview
nakv*
}
ivsp
- Sets
the value of the field of name
slotname
of the object
object
to the value
value.
If the value in the field is any other value, an error is raised. The
compliance of the new value
value
with the type of the classslot in each class to which the object is attached is
checked. If it fails, nothing is changed and the error
ivsv
is raised. If the optional set of concept views
views
is provided, the action only happens if the field is visible under at least one
of the views.
- (tr-unset-value
object slotname rest: views
) function
in [libtrp]
-> boolean,
object
object
nao,
slotname
string
nas,
ukks
,views
{ conceptview
nakv*
}
ivsp
- Resets
the value of the field of name
slotname
of the object
object.
The old value of the field, if any, is discarded. If the optional set of
concept views
views
is provided, the action only happens if the field is visible under at least one
of the views.
-
(
tr-get-value
object slotname rest: views
) function
in [libtrp]
-> value,
object
object
nao,
slotname
string
nas,
ukks
,
views
{ conceptview
nakv*
}
ivsp
- Returns
the value of the field of name
slotname
of the object
object
to the value
value.
If no value has been provided for the field, the
(unbound-slot-value)
value is returned. If the optional set of concept views
views
is provided, the action only happens if the field is visible under at least one
of the views.
- (tr-modify-value
object slotname value rest: views
) function
in [libtrp]
-> boolean,
object
object
nao,
slotname
string
nas,
ukks
,value
entity
ivsv,
cmk, kcv, ccv
,
views
{ conceptview
nakv*
}
ivsp
- Sets
the value of the field of name
slotname
of the object
object
to the value
value.
If the value in the field is any other value, no error is raised. The
compliance of the new value
value
with the type of the classslot in each class to which the object is attached is
checked. If it fails, nothing is changed and the error
ivsv
is raised. If the optional set of concept views
views
is provided, the action only happens if the field is visible under at least one
of the views.
- (tr-add-value
object slotname value rest: views
) function
in [libtrp]
-> boolean,
object
object
nao,
slotname
string
nas,
ukks,ncs
,value
entity
ivsv,
cmk, kcv, ccv
,
views
{ conceptview
nakv*
}
ivsp
- Adds
the value
value
to the value of the field of name
slotname
of the object
object.
The compliance of the value with the type of the field is checked. If it fails,
nothing is changed. If the optional set of concept views
views
is provided, the action only happens if the field is visible under at least one
of the views.
- (tr-rem-value
object slotname value rest: views
) function
in [libtrp]
-> boolean,
object
object
nao,
slotname
string
nsa,
ukks,ncs
,value
entity
ivsv,
cmk, kcv, ccv
,
views
{ conceptview
nakv*
}
ivsp
- Removes
the value
value
from the field of name
slotname
of the object
object.
The compliance of the value with the type of the field is checked. If it fails,
nothing is changed. If the optional set of concept views
views
is provided, the action only happens if the field is visible under at least one
of the views.
- (tr-mem-value
object slotname value rest: views
) function
in [libtrp]
-> boolean,
object
object
nao,
slotname
string
nsa,
ukks,ncs
,value
entity
ivsv,
views
{ conceptview
nakv*
}
ivsp
- Returns
the value
value
if it is a member of the value of the field of name
slotname
of the object
object
and
()
if it is not. If the optional set of concept views
views
is provided, the action only happens if the field is visible under at least one
of the views.
Examples
? (tr-object-p ())
= ()
? (tr-object-p (tr-create-object (tr-concept "agent") '("immo38")))
= (tr-object (tr-concept "agent") '("immo38"))
? (tr-find-object (tr-concept "agent") '("immo38"))
= (tr-object (tr-concept "agent") '("immo38"))
? (tr-create-complete-object
(tr-concept "agent")
(list (tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite")
(tr-class (tr-conceptview (tr-concept "agent") "seller") "bad"))
'(("name" . "first-immo")
("comission" . 6.5)
("area" . "grenoble")))
= (tr-object (tr-concept "agent") '("first-immo"))
? (tr-concept-instances (tr-concept "agent"))
= ((tr-object (tr-concept "agent") '("immo38"))
(tr-object (tr-concept "agent") '("first-immo")))
? (tr-class-attached (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent"))
= ((tr-object (tr-concept "agent") '("immo38")))
? (tr-class-attached (tr-class (tr-conceptview (tr-concept "agent") "buyer") "bad"))
= ()
? (tr-class-members (tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent"))
= ((tr-object (tr-concept "agent") '("immo38"))
(tr-object (tr-concept "agent") '("first-immo")))
? (tr-create-object (tr-concept "agent") '("bond, my name is bond"))
= (tr-object (tr-concept "agent") '("bond, my name is bond"))
? (tr-delete-object (tr-object (tr-concept "agent") '("bond, my name is bond")))
= t
? (tr-object-key (tr-find-object (tr-concept "agent") '("immo38")))
= ("immo38")
? (tr-object-concept (tr-find-object (tr-concept "agent") '("immo38")))
= (tr-concept "agent")
? (tr-is-in (tr-find-object (tr-concept "agent") '("immo38")))
= ((tr-class (tr-conceptview (tr-concept "agent") "buyer") "agent")
(tr-class (tr-conceptview (tr-concept "agent") "seller") "agent"))
? (tr-is-in (tr-find-object (tr-concept "agent") '("first-immo")))
= ((tr-class (tr-conceptview (tr-concept "agent") "buyer") "favorite")
(tr-class (tr-conceptview (tr-concept "agent") "seller") "bad")
? (tr-is-in-under
(tr-find-object (tr-concept "agent") '("first-immo"))
(tr-conceptview (tr-concept "agent") "seller"))
= (tr-class (tr-conceptview (tr-concept "agent") "seller") "bad")
? (tr-attach
(tr-find-object (tr-concept "agent") '("immo38"))
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "bad"))
= (tr-class (tr-conceptview (tr-concept "agent") "buyer") "bad")
? (tr-class-attached
(tr-class (tr-find-conceptview (tr-concept "agent") "buyer") "bad"))
= ((tr-object (tr-concept "agent") '("immo38")))
? (tr-is-in-under
(tr-find-object (tr-concept "agent") '("immo38"))
(tr-conceptview (tr-concept "agent") "buyer"))
= (tr-class (tr-conceptview (tr-concept "agent") "buyer") "bad")
? (tr-filtered-objects my-filter)
= ((tr-object (tr-concept "agent") '("first-immo")))
? (tr-set-classslot-domain
(tr-create-classslot my-filter "area")
(list "meylan" "montbonnot"))
= ("meylan" "montbonnot")
? (tr-filtered-objects my-filter)
= ()
? (tr-get-value (tr-object (tr-concept "agent") '("immo38")) "area")
= #s(<undef>)
? (tr-set-value (tr-object (tr-concept "agent") '("immo38")) "area" "saint-egreve")
= (tr-object (tr-concept "agent") '("immo38"))
? (tr-get-value (tr-object (tr-concept "agent") '("immo38")) "area")
= "saint-egreve"
? (tr-modify-value (tr-object (tr-concept "agent") '("immo38")) "area" "grenoble")
= (tr-object (tr-concept "agent") '("immo38"))
? (tr-get-value (tr-object (tr-concept "agent") '("immo38")) "area")
= "grenoble"
? (tr-unset-value (tr-object (tr-concept "agent") '("immo38")) "area")
= (tr-object (tr-concept "agent") '("immo38"))
? (tr-get-value (tr-object (tr-concept "agent") '("immo38")) "houses")
= #s(<undef>)
? (tr-get-value (tr-object (tr-concept "agent") '("immo38")) "houses")
= #s(<undef>)
? (tr-set-value (tr-object (tr-concept "agent") '("immo38")) "houses"
(list (tr-object (tr-concept "house") '("meylan" 176 3))))
= (tr-object (tr-concept "agent") '("immo38"))
? (tr-add-value (tr-object (tr-concept "agent") '("immo38")) "houses"
(tr-object (tr-concept "house") '("rue Monge" 3 2)))
= (tr-object (tr-concept "agent") '("immo38"))
? (tr-mem-value
(tr-object (tr-concept "agent") '("immo38"))
"houses"
(tr-object (tr-concept "house") '("rue Monge" 3 2)))
= ((tr-object (tr-concept "house") '("rue Monge" 3 2)))
? (tr-rem-value
(tr-object (tr-concept "agent") '("immo38"))
"houses"
(tr-object (tr-concept "house") '("meylan" 176 3)))
= (tr-object (tr-concept "agent") '("immo38"))
? (tr-get-value
(tr-object (tr-concept "agent") '("immo38"))
"houses")
= ((tr-object (tr-concept "house") '("rue Monge" 3 2)))
Annotations
The
current version of
TROEPS
contains a very rough mechanism for annotating fields and objects. Thus, any
TROEPS
entity and any object field can receive annotations. Users may declare labels
for annotations (preventing the concurrent use of the same label), assign and
retrieve annotations in fields objects. The current implementation does not
provide any mechanism for securing annotations (setting an annotation erases
any previous value for it). So, using annotations requires a great deal of
programming. However, the annotation system, when unused, adds only one
additional field per object and does not waste additional time but for
allocating memory.
The
set of already reserved annotation is presented in Appendix
9.
Typed
annotations are saved in a file which extension is
.adf.
Others are not saved.
API
- (tr-declare-annotation
label
comment optional: type const
) function
in [libtrp]
->
label,
label
string
nas,ada,
comment
string
nas,
type
string|concept
ivt,
const
string
nas,
ivc
- Declares
the label
label
for annotating objects, raise an error if the label is already declared. If no
type and constructor is given the annotation will simply not be saved.
- (tr-declared-annotation-p
label) function
in [libtrp]
->
string|(),
label
string
nas
- Checks
if the label
label
is declared for annotations. If so, returns its comment otherwise returns
().
- (tr-set-slot-annotation
object
slotname label annotation
) function
in [libtrp]
-> object,
object
object
nao,
slotname
string
nas,ukks,
label
string
nas,naa,
annotation
entity
,
bta
- Sets
the annotation
annotation
under the label
label
for the field
slotname
of the object
object.
This primitive does not check whether there is already a value or not: it just
replaces it.
- (tr-get-slot-annotation
object
slotname label
) function
in [libtrp]
-> object,
object
object
nao,
slotname
string
nas,ukks,
label
string
nas,naa
- Gets
and returns the annotation under the label
label
for the field
slotname
of the object
object.
Returns
()
if no such annotation is defined.
- (tr-rem-slot-annotation
object
slotname label
) function
in [libtrp]
-> object,
object
object
nao,
slotname
string
nas,ukks,
label
string
nas,naa
- Erases
the annotation under the label
label
for the field
slotname
of the object
object.
The
following primitives allow to annotate any of the
TROEPS
entities defined above (base, concepts, viewpoints, classes, instances, etc.).
- (tr-set-annotation
entity
label annotation
) function
in [libtrp]
-> entity,
entity
entity
nao,
label
string
nas,naa,
annotation
entity
,
bta
- Sets
the annotation
annotation
under the label
label
for the entity
entity.
This primitive does not check whether there is already a value or not: it just
replaces it.
- (tr-get-annotation
entity
label
) function
in [libtrp]
-> entity,
entity
entity
nao,
label
string
nas,naa
- Gets
and returns the annotation under the label
label
for the entity
entity.
Returns
()
if no such annotation is defined.
- (tr-rem-annotation
entity
label
) function
in [libtrp]
-> entity,
entity
entity
nao,
label
string
nas,naa
- Erases
the annotation under the label
label
for the entity
entity.
Examples
? (tr-declared-annotation-p "my-opinion")
= ()
? (tr-declare-annotation "my-opinion" "Here is my opinion on the considered item")
= "Here is my opinion on the considered item"
? (tr-declared-annotation-p "my-opinion")
= "Here is my opinion on the considered item"
? (tr-set-annotation
(tr-class (tr-conceptview (tr-concept "agent") "buyer") "good")
"my-opinion"
"Here I put good agents as far as I can judge")
= "Here I put good agents as far as I can judge"
? (tr-set-annotation
(tr-object (tr-concept "agent") '("first-immo"))
"my-opinion"
"Not really the first, but at least, not the last")
= "Not really the first, but at least, not the last"
? (tr-get-annotation
(tr-object (tr-concept "agent") '("first-immo"))
"my-opinion")
= "Not really the first, but at lest, not the last")
? (tr-rem-annotation
(tr-object (tr-concept "agent") '("first-immo"))
"my-opinion")
= ()
? (tr-get-annotation
(tr-object (tr-concept "agent") '("first-immo"))
"my-opinion")
= ()
? (tr-set-slot-annotation
(tr-object (tr-concept "agent") '("first-immo"))
"area"
"my-opinion"
'("the agent lives in area" "saint-egreve"))
= ("the agent lives in area" "saint-egreve")
? (tr-get-slot-annotation
(tr-object (tr-concept "agent") '("first-immo"))
"area"
"my-opinion")
= ("the agent lives in area" "saint-egreve")
? (tr-rem-slot-annotation
(tr-object (tr-concept "agent") '("first-immo"))
"area"
"my-opinion")
= ()
? (tr-get-slot-annotation
(tr-object (tr-concept "agent") '("first-immo"))
"area"
"my-opinion")
= ()
Lexicon
Facility
for manipulating a lexicon has been added to the
TROEPS
system. The lexicon helps both the designer and the user of a knowledge base in
providing the definitions of the terms used in the knowledge base (as
identifiers) and relating these terms.
Description
of lexicon elements
A
lexicon is a simple set of lexitems. Each lexitem represents a particular term.
It is characterised by the following information:
- its
name which corresponds to the term itself (e.g., house);
- its
definition which is a string defining the term (e.g. a building in which
people, usually one family, live in);
- its
hyperonym which is a lexitem representing a term more general than the current
one (e.g. building);
- its
hyponyms which are lexitems representing terms more specific than the current
one (e.g. semi-detached house, cottage);
- its
synonyms which are other lexitem representing terms with the same meaning (e.g.
apartment for flat);
- its
antonyms which are other lexitem representing terms with opposite meanings
(e.g. non furnished for furnished);
- its
bibliography which is set of bibliographic references (unspecified) related to
the term (e.g. the place where the definition has been found: "Cambridge
international dictionary of English, Cambridge university press, Cambridge
(UK), 1995");
- its
related objects which are
TROEPS
entities implementing in one sense or another the term (e.g. the
house
concept and all the root classes of this concept).
The
relationship between these components of lexitems are managed correctly, for
instance, if furnished is declared as an antonym of non furnished then non
furnished is an antonym of furnished (however, if symmetry is dealt with
correctly, this is not the case for transitivity neither for synonyms nor
hyponyms).
Linking
lexicon elements to TROEPS objects
Lexicons
can be saved in files and loaded at any time. They can also be linked to the
entities of a knowledge base. This means that for any entity, if its name is a
term corresponding to a lexitem, then the entity will be added to the related
objects of the lexitem and the lexitem will be considered as the lexical
equivalent of the entity (there can be several entities related to a lexitem
while there is only one lexitem connected with an entity).
A
knowledge base can have one or several lexicons attached to it. This means that
at knowledge base load time, the lexicon will be loaded and the knowledge base
will be indexed by the terms in the lexicons.
Interface

Screendump
36: Lexicon home page.
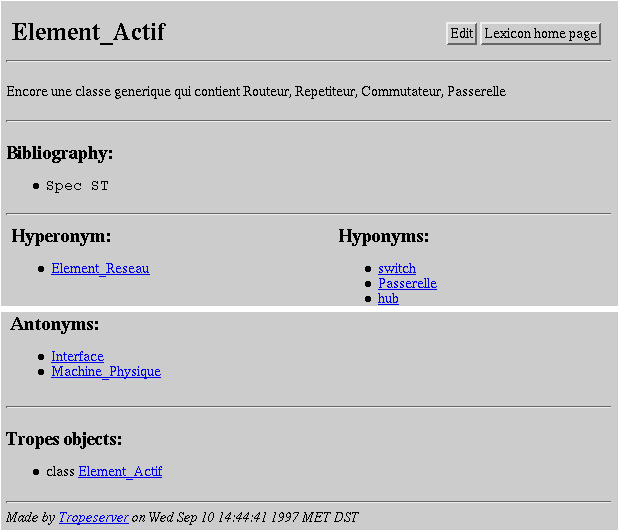
Screendump
37: Lexitem display.
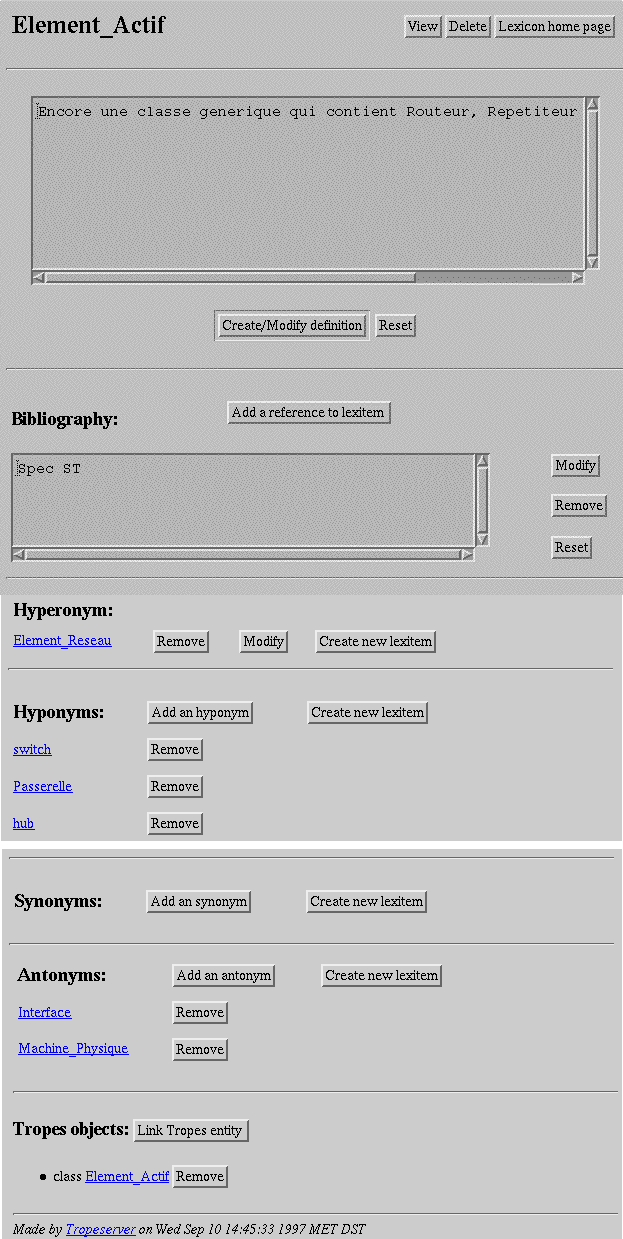
Screendump
38: Lexitem edition.
Screendump
39: Lexitem creation.
API
- (tr-load-lexicon
filename
optional: print
) function
in [libtrp]
-> boolean,
filename
filename
naf,fnf,
print
boolean
- Loads
the lexicon contained in file
filename.
- (tr-save-lexicon
filename) function
in [libtrp]
-> boolean,
filename
filename
naf
- Saves
all the lexitems contained in the environment in the file
filename.
- (tr-lexitem-p
anything) function
in [libtrp]
->
boolean,
anything
entity
- Returns
anything
if the argument
anything
is a lexitem,
()
otherwise.
- (tr-create-lexitem
name
hyperonym
) function
in [libtrp]
-> lexitem,
name
string
nas,
hyperonyms
()|lexitem
nali
- Creates
a lexitem corresponding to a term. It has
name
for name and
hyperonym
for hyperorym if there are specified.
- (tr-find-lexitem
name) function
in [libtrp]
-> lexitem,
name
string
nas
- Finds
the lexitem corresponding to the term
name.
- (tr-delete-lexitem
lexitem) function
in [libtrp]
->
boolean,
lexitem
lexitem
nali
- Deletes
the lexitem
lexitem.
- (tr-lexitem-name
lexitem) function
in [libtrp]
->
string,
lexitem
lexitem
nali
- Returns
the name of the lexitem
lexitem.
- (tr-lexitem-rename
lexitem
name
) function
in [libtrp]
->
string,
lexitem
lexitem
nali,
name
string
nas,adl
- Returns
the name of the lexitem
lexitem.
- (tr-lexitem-definition
lexitem) function
in [libtrp]
->
string,
lexitem
lexitem
nali
- Returns
the definition of the lexitem
lexitem.
- (tr-lexitem-hyperonym
lexitem) function
in [libtrp]
->
lexitem,
lexitem
lexitem
nali
- Returns
the hyperonym of the lexitem
lexitem.
- (tr-lexitem-hyponyms
lexitem) function
in [libtrp]
->
( lexitem* ),
lexitem
lexitem
nali
- Returns
the hyponyms of the lexitem
lexitem.
- (tr-lexitem-synonyms
lexitem) function
in [libtrp]
->
( lexitem* ),
lexitem
lexitem
nali
- Returns
the synonyms of the lexitem
lexitem.
- (tr-lexitem-antonyms
lexitem) function
in [libtrp]
->
( lexitem* ),
lexitem
lexitem
nali
- Returns
the antonyms of the lexitem
lexitem.
- (tr-lexitem-bibliography
lexitem) function
in [libtrp]
->
( string* ),
lexitem
lexitem
nali
- Returns
the bibliographic references of the lexitem
lexitem.
- (tr-lexitem-objects
lexitem) function
in [libtrp]
->
( entity* ),
lexitem
lexitem
nali
- Returns
the
TROEPS
entities related to the lexitem
lexitem.
- (tr-lexitem-set-hyperonym
lexitem
hyperonym
) function
in [libtrp]
->
lexitem,
lexitem
lexitem
nali,
hyperlexitemnali
- Sets
the hyperonym of the lexitem
lexitem
to be the lexitem
hyperonym.
- (tr-lexitem-set-definition
lexitem
definition
) function
in [libtrp]
->
lexitem,
lexitem
lexitem
nali,
definition
stringnas
- Sets
the definition of the lexitem
lexitem
to be the string
definition.
- (tr-lexitem-add-hyponym
lexitem
hyponym
) function
in [libtrp]
->
lexitem,
lexitem
lexitem
nali,
hyponym
lexitemnali
- Add
the lexitem
hyponym
in the hyponyms of the lexitem
lexitem.
- (tr-lexitem-add-synonym
lexitem
synonym
) function
in [libtrp]
->
lexitem,
lexitem
lexitem
nali,
synonym
lexitemnali
- Adds
the lexitem
synonym
in the synonyms of the lexitem
lexitem.
- (tr-lexitem-add-antonym
lexitem
antonym
) function
in [libtrp]
->
lexitem,
lexitem
lexitem
nali,
antonym
lexitemnali
- Adds
the lexitem
antonym
in the antonyms of the lexitem
lexitem.
- (tr-lexitem-add-bibliography
lexitem
bibliography
) function
in [libtrp]
->
lexitem,
lexitem
lexitem
nali,
bibliography
string
- Adds
the bibliographic reference
bibliography
in the bibliography of the lexitem
lexitem.
- (tr-lexitem-add-object
lexitem
object
) function
in [libtrp]
->
lexitem,
lexitem
lexitem
nali,
object
entitynao
- Adds
the entity
object
in the related objects of the lexitem
lexitem.
- (tr-lexitem-rem-hyponym
lexitem
hyponym
) function
in [libtrp]
->
lexitem,
lexitem
lexitem
nali,
hyponym
lexitemnali
- Removes
the lexitem
hyponym
from the hyponyms of the lexitem
lexitem.
- (tr-lexitem-rem-synonym
lexitem
synonym
) function
in [libtrp]
->
lexitem,
lexitem
lexitem
nali,
synonym
lexitemnali
- Removes
the lexitem
synonym
from the synonyms of the lexitem
lexitem.
- (tr-lexitem-rem-antonym
lexitem
antonym
) function
in [libtrp]
->
lexitem,
lexitem
lexitem
nali,
antonym
lexitemnali
- Removes
the lexitem
antonym
from the antonyms of the lexitem
lexitem.
- (tr-lexitem-rem-bibliography
lexitem
bibliography
) function
in [libtrp]
->
lexitem,
lexitem
lexitem
nali,
bibliography
string
- Removes
the bibliographic reference
bibliography
from the bibliography of the lexitem
lexitem.
- (tr-lexitem-rem-object
lexitem
object
) function
in [libtrp]
->
lexitem,
lexitem
lexitem
nali,
object
entitynao
- Removes
the entity
object
from the related objects of the lexitem
lexitem.
- (tr-attach-lexicon
base) function
in [libtrp]
-> entity,
base
base
nab
- Attaches
to each entity contained in the base base the lexitem corresponding to it.
- (tr-get-lexitem
entity) function
in [libtrp]
-> lexitem,
entity
entity
nao
- Returns
the lexitem attached to a particular
TROEPS
entity
entity
(
()
if none is attached).
Example
? (tr-create-lexitem `house ())
= (tr-lexitem "house")
? (tr-lexitem-name (tr-find-lexitem "house"))
= "house"
? (tr-lexitem-set-definition (tr-find-lexitem "house")
"a building in which people, usually one familly, live in")
= "a building in which people, usually one familly, live in"
? (tr-lexitem-definition (tr-find-lexitem "house"))
= "a building in which people, usually one familly, live in"
? (tr-lexitem-add-bibliography (tr-find-lexitem "house")
"Cambridge international dictionary of English, Cambridge university press, Cambridge (UK), 1995"))
= ("Cambridge international dictionary of English, Cambridge university press, Cambridge (UK), 1995")
? (tr-lexitem-bibliography (tr-find-lexitem "house"))
= ("Cambridge international dictionary of English, Cambridge university press, Cambridge (UK), 1995")
? (tr-lexitem-set-hyperonym (tr-find-lexitem "house")
(tr-create-lexitem `building ()))
= (tr-lexitem "house")
? (tr-lexitem-hyperonym (tr-find-lexitem "house"))
= (tr-lexitem "building")
? (tr-lexitem-hyponyms (tr-find-lexitem "building"))
= ((tr-lexitem "house"))
? (tr-lexitem-add-hyponym (tr-find-lexitem "building")
(tr-create-lexitem `flat ()))
= ((tr-lexitem "flat")(tr-lexitem "house"))
? (tr-lexitem-hyperonyms (tr-find-lexitem "flat"))
= ()
? (tr-lexitem-hyponyms (tr-find-lexitem "building"))
= ((tr-lexitem "flat")(tr-lexitem "house"))
? (tr-lexitem-add-synonym (tr-find-lexitem "flat")
(tr-create-lexitem `appartment ()))
= ((tr-lexitem "flat"))
? (tr-lexitem-synonyms (tr-find-lexitem "flat"))
= ((tr-lexitem "appartment"))
? (tr-lexitem-synonyms (tr-find-lexitem "appartment"))
= ((tr-lexitem "flat"))
? (tr-lexitem-add-antonym (tr-create-lexitem `furnished ()))
(tr-create-lexitem `non furnished ()))
= ((tr-lexitem "furnished"))
? (tr-lexitem-antonyms (tr-find-lexitem "furnished"))
= ((tr-lexitem "non furnished"))
? (tr-lexitem-antonyms (tr-find-lexitem "non furnished"))
= ((tr-lexitem "furnished"))
? (tr-attach-lexicon (tr-base "real-estate"))
= t
? (tr-lexitem-objects (tr-find-lexitem "house"))
= ((tr-class (tr-conceptview (tr-concept "house") "price") "house")
(tr-class (tr-conceptview (tr-concept "house") "test") "house")
(tr-class (tr-conceptview (tr-concept "house") "size") "house")
(tr-class (tr-conceptview (tr-concept "house") "localisation") "house")
(tr-concept "house"))
? (tr-get-lexitem (tr-concept "house"))
= (tr-lexitem "house")
? (tr-lexitem-add-object (tr-find-lexitem "house")
(tr-object (tr-concept "house") `("rue Monge" 2 3))))
= (tr-lexitem "house")
? (tr-lexitem-objects (tr-find-lexitem "house"))
= ((tr-object (tr-concept "house") `("rue Monge" 2 3))
(tr-class (tr-conceptview (tr-concept "house") "price") "house")
(tr-class (tr-conceptview (tr-concept "house") "test") "house")
(tr-class (tr-conceptview (tr-concept "house") "size") "house")
(tr-class (tr-conceptview (tr-concept "house") "localisation") "house")
(tr-concept "house"))
? (tr-save-lexicon #f"real-estate.ldf")
= ()
? (tr-lexitem-rem-object (tr-find-lexitem "house") (tr-concept "house"))
= (tr-lexitem "house")
? (tr-lexitem-objects (tr-find-lexitem "house"))
= ((tr-object (tr-concept "house") `("rue Monge" 2 3))
(tr-class (tr-conceptview (tr-concept "house") "price") "house")
(tr-class (tr-conceptview (tr-concept "house") "test") "house")
(tr-class (tr-conceptview (tr-concept "house") "size") "house")
(tr-class (tr-conceptview (tr-concept "house") "localisation") "house"))
? (tr-lexitem-rem-synonym (tr-find-lexitem "flat") (tr-find-lexitem "appartment"))
= ()
? (tr-lexitem-synonyms (tr-find-lexitem "appartment"))
= ()
? (tr-lexitem-rem-antonym (tr-find-lexitem "furnished") (tr-find-lexitem "non furnished"))
= ()
? (tr-lexitem-antonyms (tr-find-lexitem "non furnished"))
= ()
? (tr-lexitem-rem-bibliography (tr-find-lexitem "house")
"Cambridge international dictionary of English, Cambridge university press, Cambridge (UK), 1995")
= ()
? (tr-lexitem-bibliography (tr-find-lexitem "house"))
= ()
? (tr-lexitem-rem-hyponym (tr-find-lexitem "building") (tr-find-lexitem "flat"))
= ()
? (tr-lexitem-hyperonym (tr-find-lexitem "flat"))
= ()
? (tr-delete-lexitem "house")
= t
? (tr-find-lexitem "house")
= ()
? (tr-load-lexicon #f"real-estate.ldf")
= ()
? (tr-find-lexitem "house")
= (tr-lexicon "house")


















































